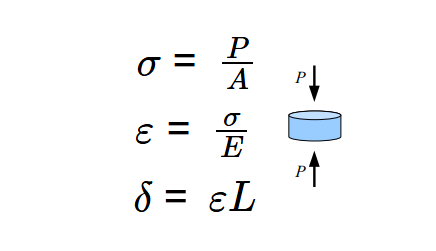1. What is the Compression Calculator?

Definition: The Compression Calculator determines the stress, strain, and deflection of a cylinder under a load using the formulas \( \sigma = \frac{P}{A} \), \( \varepsilon = \frac{\sigma}{E} \), and \( \delta = \varepsilon L \), where \(P\) is the load, \(A\) is the cross-sectional area, \(E\) is Young's modulus, and \(L\) is the length.

Purpose: Helps engineers analyze how a cylinder deforms under load (tensile or compressive).

Reference:Applied Strength of Materials for Engineering Technology

http://www.etcs.pfw.edu/~dupenb/ET_200/Applied%20Str%20of%20Mat%20for%20ET%20v14%20July%202018.pdf

2. How Does the Calculator Work?

Formulas:

Where:

• \(\sigma\): Stress (MPa)
• \(P\): Load (kN, positive for tensile, negative for compressive)
• \(A\): Cross-sectional area (\( \pi d^2 / 4 \), cm²)
• \(\varepsilon\): Strain
• \(E\): Young's modulus (GPa)
• \(\delta\): Deflection (cm)
• \(L\): Length (cm)

Steps:

• Step 1: Input Load. Enter the load with sign (e.g., 70 kN for tensile, -70 kN for compressive).
• Step 2: Input Diameter. Enter the cylinder diameter (e.g., 5 cm).
• Step 3: Input Length. Enter the length (e.g., 3 cm).
• Step 4: Input Young's Modulus. Enter the modulus (e.g., 207 GPa).
• Step 5: Calculate. The calculator computes stress, strain, and deflection based on the load sign.

3. Importance of Load Calculation

Calculating load effects is crucial for:

• Structural Integrity: Ensures the cylinder can withstand deformation.
• Material Analysis: Assesses material behavior under tensile or compressive loads.
• Unit Consistency: Supports conversions across load, diameter, and length units.

4. Using the Calculator

Example 1 (Compressive): Load = -70 kN, Diameter = 5 cm, Length = 3 cm, Young's Modulus = 207 GPa:

• Step 1: \(P = -70 \, \text{kN}\).
• Step 2: \(A = \pi (2.5)^2 = 19.63 \, \text{cm}^2\).
• Step 3: \(\sigma = \frac{-70}{19.63} \cdot 10 = -35.6 \, \text{MPa}\).
• Step 4: \(\varepsilon = \frac{-35.6}{207} = -0.000172\).
• Step 5: \(\delta = -0.000172 \cdot 3 = -0.00052 \, \text{cm}\).

Example 2 (Tensile): Load = 70 kN, Diameter = 5 cm, Length = 3 cm, Young's Modulus = 207 GPa:

• Step 1: \(P = 70 \, \text{kN}\).
• Step 2: \(A = \pi (2.5)^2 = 19.63 \, \text{cm}^2\).
• Step 3: \(\sigma = \frac{70}{19.63} \cdot 10 = 35.6 \, \text{MPa}\).
• Step 4: \(\varepsilon = \frac{35.6}{207} = 0.000172\).
• Step 5: \(\delta = 0.000172 \cdot 3 = 0.00052 \, \text{cm}\).

5. Frequently Asked Questions (FAQ)

Q: What does the load sign mean?
A: Positive load indicates tension, negative load indicates compression.

Q: Why convert units?
A: The calculator ensures consistent units with a conversion factor to MPa.

Q: Is this accurate for all cylinders?
A: Yes, if the load, diameter, length, and modulus are correctly measured.