Steel Block Strain Calculator - Calculate the strains in the x, y, and z

Load in x-direction (P_x):

Load in y-direction (P_y):

Load in z-direction (P_z):

Length in x-direction:

Length in y-direction:

Length in z-direction:

Young's Modulus (E):

Poisson's Ratio (ν):

Stress in x-direction (σ_x):

Stress in y-direction (σ_y):

Stress in z-direction (σ_z):

Strain in x-direction (ε_x):

Strain in y-direction (ε_y):

Strain in z-direction (ε_z):

Unit Converter ▲

Unit Converter ▼

From:	To:

1. What is the Steel Block Strain Calculator?

Definition: The Steel Block Strain Calculator determines the normal stresses and strains in the \(x\), \(y\), and \(z\) directions for a steel block under applied loads.

Purpose: Helps engineers analyze the deformation of steel blocks under multi-axial loading.

Reference:Applied Strength of Materials for Engineering Technology

http://www.etcs.pfw.edu/~dupenb/ET_200/Applied%20Str%20of%20Mat%20for%20ET%20v14%20July%202018.pdf

2. How Does the Calculator Work?

Formula:

\(\sigma_i = \frac{P_i}{A_j \cdot A_k}\), \(\epsilon_i = \frac{1}{E} [\sigma_i - \nu (\sigma_j + \sigma_k)]\)

Where:

\(\sigma_i\): Normal stress in direction \(i\) (MPa)
\(P_i\): Load in direction \(i\) (N)
\(A_j, A_k\): Perpendicular areas (cm²)
\(\epsilon_i\): Strain in direction \(i\)
\(E\): Young's modulus (Pa)
\(\nu\): Poisson's ratio

Steps:

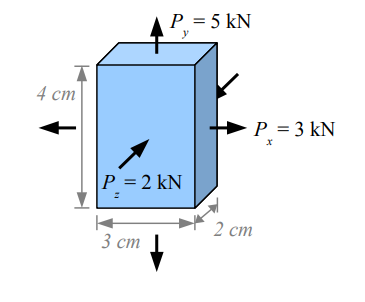
Step 1: Input Loads. Enter the loads in \(x\), \(y\), and \(z\) directions (e.g., 3 kN, 5 kN, -2 kN).
Step 2: Input Dimensions. Enter the block dimensions in \(x\), \(y\), and \(z\) directions (e.g., 4 cm, 3 cm, 2 cm).
Step 3: Input Young's Modulus. Enter the modulus (e.g., 207 GPa).
Step 4: Input Poisson's Ratio. Enter the ratio (e.g., 0.25).
Step 5: Calculate. The calculator computes stresses and strains.

3. Importance of Stress and Strain Calculation

Calculating stresses and strains is crucial for:

Material Strength: Ensures the block can withstand the loads.
Design Optimization: Helps determine appropriate dimensions.
Deformation Analysis: Assesses potential deformation under load.

4. Using the Calculator

Example: Load \(P_x = 3 \, \text{kN}\), \(P_y = 5 \, \text{kN}\), \(P_z = -2 \, \text{kN}\), Dimensions = 4 cm × 3 cm × 2 cm, \(E = 207 \, \text{GPa}\), \(\nu = 0.25\):

Step 1: \(\sigma_x = \frac{3000}{3 \cdot 2} = 500 \, \text{N/cm}^2 = 5 \, \text{MPa}\).
Step 2: \(\sigma_y = \frac{5000}{4 \cdot 2} = 625 \, \text{N/cm}^2 = 6.25 \, \text{MPa}\).
Step 3: \(\sigma_z = \frac{-2000}{4 \cdot 5} = -100 \, \text{N/cm}^2 = -1.67 \, \text{MPa}\) (corrected area to 4×3=12 cm²).
Step 4: \(\epsilon_x = \frac{1}{207 \cdot 10^9} [5 \cdot 10^6 - 0.25 (6.25 \cdot 10^6 - 1 \cdot 10^6)] \approx 1.86 \times 10^{-5}\).
Step 5: \(\epsilon_y = \frac{1}{207 \cdot 10^9} [6.25 \cdot 10^6 - 0.25 (5 \cdot 10^6 - 1 \cdot 10^6)] \approx 2.62 \times 10^{-5}\).
Step 6: \(\epsilon_z = \frac{1}{207 \cdot 10^9} [-1 \cdot 10^6 - 0.25 (5 \cdot 10^6 + 6.25 \cdot 10^6)] \approx -2.16 \times 10^{-5}\).

5. Frequently Asked Questions (FAQ)

Q: What is normal stress?
A: Normal stress is the force per unit area acting perpendicular to a surface.

Q: Can I use different units?
A: Yes, the calculator converts N to kN and mm to cm internally.

Q: Is this accurate for all materials?
A: Yes, if \(E\) and \(\nu\) are correctly input for the material.