Star to Delta Conversion Calculator

Star Resistance \( R1 \) (Ω): ⓘ

Star Resistance \( R2 \) (Ω): ⓘ

Star Resistance \( R3 \) (Ω): ⓘ

Delta Resistance \( R_a \) (Ω):

Delta Resistance \( R_b \) (Ω):

Delta Resistance \( R_c \) (Ω):

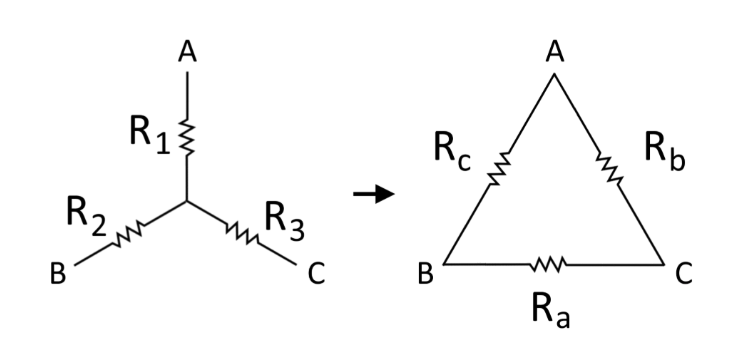
1. What is Star-to-Delta Conversion?

Definition: Star-to-Delta conversion, also known as Wye-to-Delta or Y-Δ transformation, is a technique used in electrical engineering to convert a star (Y) configuration of resistors into an equivalent delta (Δ) configuration. This transformation simplifies the analysis of three-phase circuits.

Purpose: This calculator converts star-connected resistances into their delta equivalents, which is essential for simplifying complex three-phase circuits in power systems, electrical networks, and RF applications.

2. How Does the Calculator Work?

The calculator uses the following formulas for star-to-delta conversion:

Delta Resistances:
\[ \begin{aligned} R_a &= \frac{R1 \cdot R2 + R2 \cdot R3 + R3 \cdot R1}{R1} \\ R_b &= \frac{R1 \cdot R2 + R2 \cdot R3 + R3 \cdot R1}{R2} \\ R_c &= \frac{R1 \cdot R2 + R2 \cdot R3 + R3 \cdot R1}{R3} \end{aligned} \]

Where:

\( R_a \), \( R_b \), \( R_c \): Delta-connected resistances (in ohms, \( \Omega \))
\( R1 \), \( R2 \), \( R3 \): Star-connected resistances (in ohms, \( \Omega \))

Steps:

Enter the star-connected resistances \( R1 \), \( R2 \), and \( R3 \) in ohms.
Click "Calculate" to compute the equivalent delta-connected resistances \( R_a \), \( R_b \), and \( R_c \).
Results are displayed in ohms with 4 decimal places, or in scientific notation if less than 0.001.

3. Importance of Star-to-Delta Conversion

Star-to-Delta conversion is crucial for:

Circuit Simplification: Converts complex three-phase networks into simpler forms for analysis.
Power Systems: Facilitates the design and analysis of three-phase power systems by transforming impedances.
RF Applications: Assists in impedance matching and network analysis in high-frequency circuits.

4. Using the Calculator

Examples:

Example 1: Equal Star Resistances
- \( R1 = 10 \, \Omega \), \( R2 = 10 \, \Omega \), \( R3 = 10 \, \Omega \)
- Common term: \( 10 \times 10 + 10 \times 10 + 10 \times 10 = 300 \)
- \( R_a = \frac{300}{10} = 30.0000 \, \Omega \)
- \( R_b = \frac{300}{10} = 30.0000 \, \Omega \)
- \( R_c = \frac{300}{10} = 30.0000 \, \Omega \)
Example 2: Unequal Star Resistances
- \( R1 = 5 \, \Omega \), \( R2 = 10 \, \Omega \), \( R3 = 15 \, \Omega \)
- Common term: \( 5 \times 10 + 10 \times 15 + 15 \times 5 = 50 + 150 + 75 = 275 \)
- \( R_a = \frac{275}{5} = 55.0000 \, \Omega \)
- \( R_b = \frac{275}{10} = 27.5000 \, \Omega \)
- \( R_c = \frac{275}{15} \approx 18.3333 \, \Omega \)
Example 3: Small Resistances
- \( R1 = 2 \, \Omega \), \( R2 = 3 \, \Omega \), \( R3 = 4 \, \Omega \)
- Common term: \( 2 \times 3 + 3 \times 4 + 4 \times 2 = 6 + 12 + 8 = 26 \)
- \( R_a = \frac{26}{2} = 13.0000 \, \Omega \)
- \( R_b = \frac{26}{3} \approx 8.6667 \, \Omega \)
- \( R_c = \frac{26}{4} = 6.5000 \, \Omega \)

5. Frequently Asked Questions (FAQ)

Q: What is the difference between star and delta configurations?
A: In a star (Y) configuration, resistors are connected in an open "Y" shape with a common node, while in a delta (Δ) configuration, resistors form a closed loop in a triangular shape.

Q: Why perform star-to-delta conversion?
A: Converting a star configuration to delta can simplify the analysis of three-phase circuits, especially when dealing with parallel impedances or simplifying network calculations.

Q: Are the converted delta resistances always larger than the star resistances?
A: Yes, typically the delta resistances are larger because the conversion involves summing products of the star resistances, which increases the equivalent resistance.