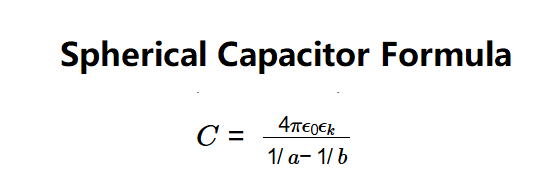Spherical Capacitor Calculator

Inner Radius (\( a \)):

Outer Radius (\( b \)):

Relative Permittivity (\( \epsilon_k \)):

1. What is Spherical Capacitor Calculator?

Definition: This calculator computes the capacitance (\( C \)) of a spherical capacitor, which consists of two concentric spherical shells separated by a dielectric material.

Purpose: It is used in physics and electrical engineering to determine the capacitance of spherical capacitors, which are relevant in theoretical studies, high-voltage applications, and certain types of sensors.

2. How Does the Calculator Work?

The calculator uses the following formula for the capacitance of a spherical capacitor:

\( C = \frac{4 \pi \epsilon_0 \epsilon_k}{1/a - 1/b} \)

Where:

\( C \): Capacitance (F);
\( \epsilon_0 = 8.85 \times 10^{-12} \, \text{F/m} \): Vacuum permittivity;
\( \epsilon_k \): Relative permittivity of the dielectric (unitless);
\( a \): Radius of the inner sphere (m);
\( b \): Radius of the outer sphere (m).

Steps:

Enter the inner radius (\( a \)), outer radius (\( b \)), and relative permittivity (\( \epsilon_k \)) with their units.
Convert radii to meters.
Calculate the capacitance using the formula above.
Convert the capacitance to the selected output unit (F/nF/pF).
Display the result in scientific notation if its absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Spherical Capacitor Calculation

Calculating the capacitance of a spherical capacitor is crucial for:

Theoretical Physics: Understanding the behavior of electric fields and potentials in spherical geometries, often used in educational contexts.
High-Voltage Applications: Designing capacitors for high-voltage systems where spherical geometry minimizes electric field stress.
Dielectric Studies: Analyzing the effect of dielectric materials on capacitance, which is important for material science and sensor design.

4. Using the Calculator

Example 1: Calculate the capacitance for a spherical capacitor with \( a = 5 \, \text{cm} \), \( b = 6 \, \text{cm} \), and \( \epsilon_k = 1 \):

Input Values:
\( a = 5 \, \text{cm} = 0.05 \, \text{m} \);
\( b = 6 \, \text{cm} = 0.06 \, \text{m} \);
\( \epsilon_k = 1 \);
\( \epsilon_0 = 8.85 \times 10^{-12} \, \text{F/m} \);
Denominator: \( \frac{1}{a} - \frac{1}{b} = \frac{1}{0.05} - \frac{1}{0.06} \approx 3.333 \);
Capacitance: \( C = \frac{4 \pi \epsilon_0 \epsilon_k}{\frac{1}{a} - \frac{1}{b}} = \frac{4 \pi \times (8.85 \times 10^{-12}) \times 1}{3.333} \approx 3.334 \times 10^{-11} \, \text{F} = 33.34 \, \text{pF} \);
Result: \( C = 33.3400 \, \text{pF} \).

Example 2: Calculate the capacitance for a spherical capacitor with \( a = 2 \, \text{mm} \), \( b = 3 \, \text{mm} \), and \( \epsilon_k = 4 \):

Input Values:
\( a = 2 \, \text{mm} = 0.002 \, \text{m} \);
\( b = 3 \, \text{mm} = 0.003 \, \text{m} \);
\( \epsilon_k = 4 \);
\( \epsilon_0 = 8.85 \times 10^{-12} \, \text{F/m} \);
Denominator: \( \frac{1}{a} - \frac{1}{b} = \frac{1}{0.002} - \frac{1}{0.003} \approx 166.667 \);
Capacitance: \( C = \frac{4 \pi \epsilon_0 \epsilon_k}{\frac{1}{a} - \frac{1}{b}} = \frac{4 \pi \times (8.85 \times 10^{-12}) \times 4}{166.667} \approx 2.667 \times 10^{-12} \, \text{F} = 2.667 \, \text{pF} \);
Result: \( C = 2.6670 \, \text{pF} \).

5. Frequently Asked Questions (FAQ)

Q: Why does the capacitance depend on the dielectric’s relative permittivity?
A: The relative permittivity (\( \epsilon_k \)) indicates how much the dielectric increases the capacitance compared to a vacuum. A higher \( \epsilon_k \) reduces the electric field strength between the spheres, increasing the capacitance.

Q: Why must the inner radius be less than the outer radius?
A: The inner sphere must be smaller than the outer sphere (\( a < b \)) to form a valid spherical capacitor, where the dielectric fills the space between the two concentric spheres.

Q: Can this calculator be used for spherical capacitors without a dielectric?
A: Yes, by setting \( \epsilon_k = 1 \), the calculator computes the capacitance for a spherical capacitor with a vacuum (or air) between the spheres.