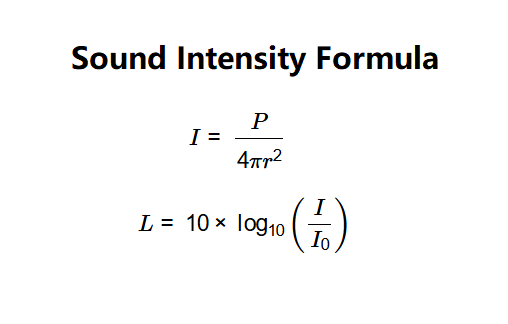Sound Intensity Calculator

Calculation Mode: ⓘ

Power \( P \): ⓘ

Area Input Mode: ⓘ

Area \( A \): ⓘ

Sound Intensity (\( I \)):

Sound Intensity Level (\( L \)):

1. What is Sound Intensity?

Definition: Sound intensity is the power per unit area carried by a sound wave, measured in watts per square meter (W/m²). The sound intensity level is a logarithmic measure of this intensity relative to a reference intensity, expressed in decibels (dB).

Purpose: This calculator helps determine the sound intensity and intensity level, which are crucial for assessing noise levels in environments like workplaces, concert venues, or residential areas, especially when the sound source's power and distance are known.

2. How Does the Calculator Work?

The calculator uses the following formulas for sound intensity calculations:

Formula 1: When Power and Area are Known
Intensity (\( I \)) = Power (\( P \)) / Area (\( A \))
\[ I = \frac{P}{A} \] In a free field, sound spreads spherically:
Area \( A \) = \( 4 \pi r^2 \)
So the sound intensity becomes:
\[ I = \frac{P}{4 \pi r^2} \]

Formula 2: To Calculate Sound Level (in Decibels)
\[ L = 10 \times \log_{10} \left( \frac{I}{I_0} \right) \]

Where:

\( I \): Sound intensity (in W/m², converted to the selected unit: W/m², mW/m², µW/m²)
\( P \): Power of the sound source (in watts, converted from W or mW)
\( A \): Area over which the sound spreads (in m², converted from m² or cm²)
\( r \): Distance from the source (in meters, converted from m or km)
\( L \): Sound level (in dB)
\( I_0 \): Reference intensity (\( 10^{-12} \, \text{W/m}^2 \), the threshold of human hearing)

Steps:

Select the calculation mode: "Power & Area/Distance to Intensity & Level", "Intensity to Level (dB)", or "Level (dB) to Intensity".
For "Power & Area/Distance": Enter the power \( P \), then choose to input either the area \( A \) or distance \( r \), selecting their units.
For "Intensity to Level": Enter the sound intensity \( I \) and select its unit (W/m², mW/m², µW/m²).
For "Level to Intensity": Enter the sound intensity level \( L \) in dB.
Click "Calculate" to compute the result.
For intensity output, select the desired unit (W/m², mW/m², µW/m²) in the result section.
Results are displayed accordingly.

3. Importance of Sound Intensity Calculations

Sound intensity calculations are essential for:

Noise Assessment: Evaluates noise levels in various environments to ensure they are within safe limits for human hearing.
Audio Engineering: Helps design audio systems by understanding how sound intensity affects perceived loudness.
Environmental Studies: Assesses the impact of noise pollution from sources like traffic or industrial equipment.

4. Using the Calculator

Examples:

Example 1: Power & Distance to Intensity & Level (Intensity in W/m²)
- \( P = 1 \, \text{W}, r = 1 \, \text{m} \)
- \( A = 4 \pi \times 1^2 \approx 12.57 \, \text{m}^2 \)
- \( I = \frac{1}{12.57} \approx 0.0796 \, \text{W/m}^2 \)
- \( L = 10 \times \log_{10} \left( \frac{0.0796}{10^{-12}} \right) \approx 109.01 \, \text{dB} \)
Example 2: Power & Area to Intensity & Level (Intensity in mW/m²)
- \( P = 100 \, \text{mW}, A = 1 \, \text{m}^2 \)
- Convert: \( P = 0.1 \, \text{W} \)
- \( I = \frac{0.1}{1} = 0.1 \, \text{W/m}^2 \)
- Output in mW/m²: \( 0.1 \times 1000 = 100 \, \text{mW/m}^2 \)
- \( L = 10 \times \log_{10} \left( \frac{0.1}{10^{-12}} \right) = 110 \, \text{dB} \)
Example 3: Level to Intensity (Output in µW/m²)
- \( L = 80 \, \text{dB} \)
- \( I = 10^{-12} \times 10^{80/10} = 10^{-12} \times 10^8 = 10^{-4} \, \text{W/m}^2 \)
- Output in µW/m²: \( 10^{-4} \times 10^6 = 100 \, \text{µW/m}^2 \)

5. Frequently Asked Questions (FAQ)

Q: What is the reference intensity \( I_0 \)?
A: The reference intensity \( I_0 = 10^{-12} \, \text{W/m}^2 \) is the threshold of human hearing, the quietest sound a human can typically hear at 1 kHz.

Q: Why use decibels for sound intensity level?
A: Decibels provide a logarithmic scale that better matches human perception of loudness, where a 10 dB increase roughly corresponds to a doubling of perceived loudness.

Q: How does unit conversion work in the calculator?
A: The calculator converts power to watts (e.g., 1000 mW = 1 W), area to m² (e.g., 10,000 cm² = 1 m²), distance to meters (e.g., 1 km = 1000 m), and intensity to/from W/m² (e.g., 1 W/m² = 1,000,000 µW/m²).