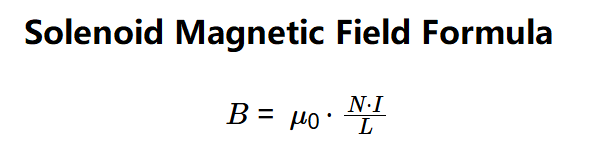Solenoid Magnetic Field Calculator

Number of Turns (\( N \)):

Electric Current (\( I \)):

Length (\( l \)):

1. What is Solenoid Magnetic Field Calculator?

Definition: This calculator computes the magnetic field (\( B \)) inside a long solenoid, which is a measure of the magnetic field strength generated by an electric current passing through the solenoid's coils.

Purpose: It is used in physics and engineering to analyze the magnetic field produced by solenoids, which are key components in electromagnets, relays, motors, and magnetic resonance imaging (MRI) systems.

2. How Does the Calculator Work?

The calculator uses the following formula for the magnetic field inside a long solenoid:

\( B = \mu_0 \cdot \frac{N \cdot I}{L} \)

Where:

\( B \): Magnetic field (T);
\( \mu_0 = 1.25664 \times 10^{-6} \, \text{T·m/A} \): Vacuum permeability;
\( N \): Number of turns;
\( I \): Electric current (A);
\( L \): Length of the solenoid (m).

Steps:

Enter the number of turns (\( N \)), electric current (\( I \)), and length (\( L \)) with their units.
Convert current to amperes and length to meters.
Calculate the magnetic field using the formula above.
Convert the magnetic field to the selected output unit (T/mT/µT).
Display the result in scientific notation if its absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Solenoid Magnetic Field Calculation

Calculating the magnetic field inside a solenoid is crucial for:

Electromagnet Design: Determining the magnetic field strength for applications like electromagnets used in MRI machines, speakers, and magnetic levitation systems.
Physics Experiments: Studying magnetic fields and their effects in laboratory settings, such as in particle accelerators.
Engineering Applications: Designing solenoids for relays, actuators, and motors that rely on magnetic fields to function.

4. Using the Calculator

Example 1: Calculate the magnetic field for a solenoid with \( N = 1000 \), \( I = 2 \, \text{A} \), and \( L = 0.5 \, \text{m} \):

Input Values:
\( N = 1000 \);
\( I = 2 \, \text{A} \);
\( L = 0.5 \, \text{m} \);
\( \mu_0 = 1.25664 \times 10^{-6} \, \text{T·m/A} \);
Magnetic Field: \( B = \mu_0 \cdot \frac{N \cdot I}{L} = (1.25664 \times 10^{-6}) \cdot \frac{1000 \cdot 2}{0.5} \approx 5.027 \times 10^{-3} \, \text{T} = 5.027 \, \text{mT} \);
Result: \( B = 5.0270 \, \text{mT} \).

Example 2: Calculate the magnetic field for a solenoid with \( N = 500 \), \( I = 10 \, \text{mA} \), and \( L = 20 \, \text{cm} \):

Input Values:
\( N = 500 \);
\( I = 10 \, \text{mA} = 0.01 \, \text{A} \);
\( L = 20 \, \text{cm} = 0.2 \, \text{m} \);
\( \mu_0 = 1.25664 \times 10^{-6} \, \text{T·m/A} \);
Magnetic Field: \( B = \mu_0 \cdot \frac{N \cdot I}{L} = (1.25664 \times 10^{-6}) \cdot \frac{500 \cdot 0.01}{0.2} \approx 3.142 \times 10^{-5} \, \text{T} = 31.42 \, \text{µT} \);
Result: \( B = 31.4200 \, \text{µT} \).

5. Frequently Asked Questions (FAQ)

Q: Why does the magnetic field depend on the number of turns?
A: The magnetic field is directly proportional to \( N \) because each turn contributes to the magnetic field, and the total field strength increases linearly with the number of turns.

Q: How does the length of the solenoid affect the magnetic field?
A: The magnetic field is inversely proportional to the length (\( L \)). A longer solenoid has a weaker magnetic field per unit length, reducing the field strength inside.

Q: Can this calculator be used for solenoids with a magnetic core?
A: This calculator assumes an air core (\( \mu = \mu_0 \)). For a magnetic core, the permeability (\( \mu \)) would need to be adjusted by multiplying \( \mu_0 \) by the relative permeability of the core material.