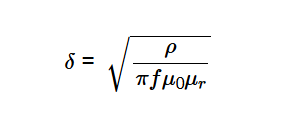Skin Depth Calculator

Material: ⓘ

Frequency \( f \): ⓘ

1. What is Skin Depth?

Definition: Skin depth (\( \delta \)) is the depth at which the amplitude of an alternating current in a conductor decreases to \( 1/e \) (about 37%) of its value at the surface, due to the skin effect in high-frequency signals.

Purpose: This calculator determines the skin depth for a conductor at a given frequency, which is critical for designing RF circuits, antennas, and cables where current tends to flow near the surface at high frequencies.

2. How Does the Calculator Work?

The calculator uses the following formula for skin depth:

Skin Depth (\( \delta \)):
\[ \delta = \sqrt{\frac{\rho}{\pi f \mu_0 \mu_r}} \]

Where:

\( \delta \): Skin depth (converted to m, mm, or µm)
\( \rho \): Resistivity (converted to \( \Omega \cdot \text{m} \) from \( \mu\Omega \cdot \text{cm} \) or \( \Omega \cdot \text{m} \))
\( f \): Frequency (converted to Hz from Hz, kHz, MHz, or GHz)
\( \mu_0 \): Permeability of free space (\( 4 \pi \times 10^{-7} \, \text{H/m} \))
\( \mu_r \): Relative permeability (unitless)

Steps:

Select a material from the dropdown or choose Custom to input your own resistivity \( \rho \) and relative permeability \( \mu_r \).
Enter the frequency \( f \) and select its unit (Hz, kHz, MHz, GHz).
Click "Calculate" to compute the skin depth.
Select the output unit for skin depth (m, mm, µm) in the result section.
The result is displayed with 4 decimal places, or in scientific notation if less than 0.001.

3. Importance of Skin Depth Calculations

Skin depth calculations are essential for:

RF Design: Determines the effective conductor thickness for high-frequency signals, affecting resistance and power loss.
Cable Selection: Helps choose appropriate conductor sizes for RF cables to minimize losses.
Antenna Efficiency: Ensures optimal performance by accounting for current distribution in antenna elements.

4. Using the Calculator

Examples:

Example 1: Copper at 1 MHz (Skin Depth in µm)
- Material: Copper (\( \rho = 1.678 \, \mu\Omega \cdot \text{cm} \), \( \mu_r = 0.999991 \))
- Frequency: \( f = 1 \, \text{MHz} = 1 \times 10^6 \, \text{Hz} \)
- Convert: \( \rho = 1.678 \times 10^{-8} \, \Omega \cdot \text{m} \)
- \( \delta = \sqrt{\frac{1.678 \times 10^{-8}}{\pi \times 1 \times 10^6 \times 4 \pi \times 10^{-7} \times 0.999991}} \approx 6.52 \times 10^{-5} \, \text{m} \)
- In µm: \( 6.52 \times 10^{-5} \times 10^6 = 65.2435 \)
Example 2: Nickel at 1 GHz (Skin Depth in µm)
- Material: Nickel (\( \rho = 6.84 \, \mu\Omega \cdot \text{cm} \), \( \mu_r = 600 \))
- Frequency: \( f = 1 \, \text{GHz} = 1 \times 10^9 \, \text{Hz} \)
- Convert: \( \rho = 6.84 \times 10^{-8} \, \Omega \cdot \text{m} \)
- \( \delta = \sqrt{\frac{6.84 \times 10^{-8}}{\pi \times 1 \times 10^9 \times 4 \pi \times 10^{-7} \times 600}} \approx 1.70 \times 10^{-6} \, \text{m} \)
- In µm: \( 1.70 \times 10^{-6} \times 10^6 = 1.6984 \)
Example 3: Custom Material at 1 kHz (Skin Depth in mm)
- Material: Custom (\( \rho = 2 \, \mu\Omega \cdot \text{cm} \), \( \mu_r = 1 \))
- Frequency: \( f = 1 \, \text{kHz} = 1 \times 10^3 \, \text{Hz} \)
- Convert: \( \rho = 2 \times 10^{-8} \, \Omega \cdot \text{m} \)
- \( \delta = \sqrt{\frac{2 \times 10^{-8}}{\pi \times 1 \times 10^3 \times 4 \pi \times 10^{-7} \times 1}} \approx 0.0021 \, \text{m} \)
- In mm: \( 0.0021 \times 10^3 = 2.1236 \)

5. Frequently Asked Questions (FAQ)

Q: What is the skin effect?
A: The skin effect is a phenomenon where alternating current tends to flow near the surface of a conductor at high frequencies, reducing the effective cross-sectional area and increasing resistance.

Q: Why does skin depth decrease with frequency?
A: Skin depth is inversely proportional to the square root of frequency (\( \delta \propto \frac{1}{\sqrt{f}} \)). As frequency increases, the current is confined to a thinner layer near the surface.

Q: How does unit conversion work in the calculator?
A: The calculator converts resistivity to \( \Omega \cdot \text{m} \) (e.g., 1 \( \mu\Omega \cdot \text{cm} \) = \( 10^{-8} \, \Omega \cdot \text{m} \)), frequency to Hz (e.g., 1 GHz = \( 10^9 \) Hz), and skin depth to the selected unit (e.g., 1 m = 1000 mm, 1 m = 1,000,000 µm).