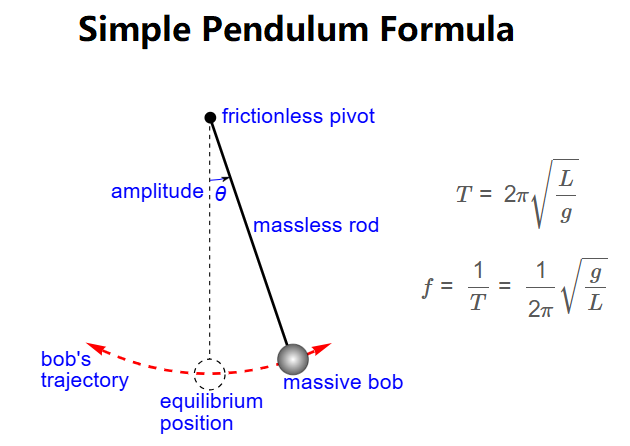
1. What is a Simple Pendulum Calculator?

Definition: This calculator computes the period ($T$) and frequency ($f$) of a simple pendulum based on its length and the acceleration due to gravity.

Purpose: It is used in physics to analyze the oscillatory motion of a simple pendulum, which is a mass suspended from a fixed point by a string, assuming small angular displacements (less than 15°).

2. How Does the Calculator Work?

The calculator uses the following formulas for a simple pendulum:

Period: $$T=2\pi \sqrt{\frac{L}{g}}$$ Frequency: $$f=\frac{1}{T}=\frac{1}{2\pi }\sqrt{\frac{g}{L}}$$ Where:

• $T$: Period (sec, min, hr)
• $f$: Frequency (Hz, kHz, MHz)
• $L$: Length of the pendulum (mm, cm, m, in, ft, yd)
• $g$: Acceleration due to gravity (m/s², ft/s²)

Unit Conversions:

• Length ($L$): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
• Acceleration due to Gravity ($g$): m/s², ft/s² (1 ft/s² = 0.3048 m/s²)
• Period ($T$): sec, min (1 min = 60 sec), hr (1 hr = 3600 sec)
• Frequency ($f$): Hz, kHz (1 Hz = 0.001 kHz), MHz (1 Hz = 0.000001 MHz)

Steps:

• Enter the length of the pendulum and the acceleration due to gravity, and select their units.
• Convert all inputs to base units (m for length, m/s² for gravity).
• Calculate the period using $T=2\pi \sqrt{\frac{L}{g}}$.
• Calculate the frequency using $f=\frac{1}{T}$.
• Convert the results to the selected units.
• Display the results, using scientific notation for values less than 0.001, otherwise with 3 decimal places.

3. Importance of Simple Pendulum Calculation

Calculating the period and frequency of a simple pendulum is crucial for:

• Physics Education: Understanding the principles of oscillatory motion and the effects of gravity.
• Engineering Applications: Designing pendulum-based devices like clocks and seismometers.
• Scientific Research: Measuring gravitational acceleration in experiments.

4. Using the Calculator

Examples:

• Example 1: For $L=1\text{m}$, $g=9.80665{\text{m/s}}^2$, period in sec, frequency in Hz:
  • Period: $T=2\pi \sqrt{\frac{1}{9.80665}}=2\pi \sqrt{0.101972}\approx 2\pi \times 0.31933\approx 2.006\text{sec}$
  • Frequency: $f=\frac{1}{2.006}\approx 0.498\text{Hz}$
• Example 2: For $L=50\text{cm}$, $g=32.17405{\text{ft/s}}^2$, period in sec, frequency in Hz:
  • Convert: $L=50\times 0.01=0.5\text{m}$, $g=32.17405\times 0.3048=9.80665{\text{m/s}}^2$
  • Period: $T=2\pi \sqrt{\frac{0.5}{9.80665}}=2\pi \sqrt{0.050986}\approx 2\pi \times 0.22581\approx 1.419\text{sec}$
  • Frequency: $f=\frac{1}{1.419}\approx 0.704\text{Hz}$

5. Frequently Asked Questions (FAQ)

Q: What is a simple pendulum?
A: A simple pendulum is a mass (bob) suspended from a fixed point by a string, oscillating under the influence of gravity, assuming small angular displacements (less than 15°).

Q: Why doesn't the period depend on the mass or amplitude?
A: For small angles, the restoring force is proportional to the displacement, and the mass cancels out in the equation of motion, making the period dependent only on the length and gravity.

Q: What is the significance of the period in real life?
A: The period of a pendulum is used in timekeeping (e.g., in pendulum clocks) and in experiments to measure gravitational acceleration.

Simple Pendulum Calculator© - All Rights Reserved 2025