Shear Strain Calculator

Input Method:

Shear Stress (\( \tau \)):

Material:

Shear Modulus (\( G \)):

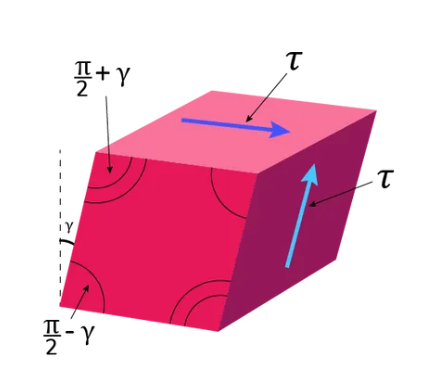
1. What is Shear Strain Calculator?

Definition: This calculator computes the shear strain (\( \gamma \)) of a material, which measures the deformation due to shear stress relative to the material's original shape.

Purpose: It is used in material science and engineering to evaluate how a material deforms under shear stress, aiding in the design of structures and components that undergo shear loading.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas:

Shear Strain (using shear stress and shear modulus): \[ \gamma = \frac{\tau}{G} \]
Shear Strain (using displacement and transverse dimension): \[ \gamma = \frac{x}{h} \]
Max Shear Strain for a Shaft Under Torsion: \[ \gamma_{\text{max}} = \frac{c \phi}{L} \] or \[ \gamma_{\text{max}} = \frac{\rho \phi}{L} \]

Where:

\( \gamma \): Shear strain (dimensionless)
\( \tau \): Shear stress (Pa, kPa, MPa, GPa, psi)
\( G \): Shear modulus (Pa, kPa, MPa, GPa, psi)
\( x \): Displacement (mm, cm, m, in, ft)
\( h \): Transverse dimension (mm, cm, m, in, ft)
\( c \) or \( \rho \): Shaft radius (mm, cm, m, in, ft)
\( \phi \): Angle of twist (radians, degrees)
\( L \): Shaft length (mm, cm, m, in, ft)

Unit Conversions:

Shear Stress (\( \tau \)) and Shear Modulus (\( G \)):
- 1 Pa = 1 Pa
- 1 kPa = 10³ Pa
- 1 MPa = 10⁶ Pa
- 1 GPa = 10⁹ Pa
- 1 psi = 6894.76 Pa
Length/Displacement (\( x \), \( h \), \( c \), \( \rho \), \( L \)):
- 1 mm = 10⁻³ m
- 1 cm = 10⁻² m
- 1 m = 1 m
- 1 in = 0.0254 m
- 1 ft = 0.3048 m
Angle (\( \phi \)):
- 1 radian = 1 radian
- 1 degree = \( \pi / 180 \) radians

Steps:

Select the input method: "Using Shear Stress and Shear Modulus", "Using Displacement and Transverse Dimension", or "Max Shear Strain for a Shaft Under Torsion".
Enter the required values with their respective units:
- For "Using Shear Stress and Shear Modulus": Enter shear stress (\( \tau \)), select a material or enter shear modulus (\( G \)).
- For "Using Displacement and Transverse Dimension": Enter displacement (\( x \)) and transverse dimension (\( h \)).
- For "Max Shear Strain for a Shaft Under Torsion": Enter shaft radius (\( \rho \)), angle of twist (\( \phi \)), and shaft length (\( L \)).
Convert all inputs to base units (Pa for stress/modulus, m for length, radians for angle).
Calculate the shear strain (\( \gamma \)) using the appropriate formula:
- If using \( \tau \) and \( G \): \( \gamma = \frac{\tau}{G} \)
- If using \( x \) and \( h \): \( \gamma = \frac{x}{h} \)
- If using \( \rho \), \( \phi \), and \( L \): \( \gamma_{\text{max}} = \frac{\rho \phi}{L} \)
Display the result with 4 decimal places.

3. Importance of Shear Strain Calculation

Calculating the shear strain is crucial for:

Material Deformation Analysis: Understanding how a material deforms under shear stress, which is essential for predicting failure and ensuring safety.
Structural Design: Ensuring that components can withstand shear deformation without failure, particularly in applications like beams, shafts, and fasteners.
Engineering Applications: Evaluating the performance of materials in real-world scenarios, such as in machinery, bridges, and buildings.

4. Using the Calculator

Example: Calculate the shear strain for a steel material with a shear stress \( \tau = 100 \, \text{MPa} \), and shear modulus \( G = 75 \, \text{GPa} \).

Select the input method as "Using Shear Stress and Shear Modulus".
Enter the shear stress, \( \tau = 100 \, \text{MPa} \).
Select the material as "Steel" (which sets \( G = 75 \, \text{GPa} \)).
The calculator computes:
- Convert \( \tau \) to Pa: \( 100 \, \text{MPa} = 100 \times 10^6 = 10^8 \, \text{Pa} \)
- Convert \( G \) to Pa: \( 75 \, \text{GPa} = 75 \times 10^9 = 7.5 \times 10^{10} \, \text{Pa} \)
- Shear strain: \( \gamma = \frac{\tau}{G} = \frac{10^8}{7.5 \times 10^{10}} = 0.001333 \)
The calculator returns:
- \( \gamma \): 0.0013

Example (Torsion): Calculate the maximum shear strain for a shaft with radius \( \rho = 10 \, \text{mm} \), angle of twist \( \phi = 2 \, \text{degrees} \), and length \( L = 1 \, \text{m} \).

Select the input method as "Max Shear Strain for a Shaft Under Torsion".
Enter the shaft radius, \( \rho = 10 \, \text{mm} \).
Enter the angle of twist, \( \phi = 2 \, \text{degrees} \).
Enter the shaft length, \( L = 1 \, \text{m} \).
The calculator computes:
- Convert \( \rho \) to m: \( 10 \, \text{mm} = 0.01 \, \text{m} \)
- Convert \( \phi \) to radians: \( 2 \, \text{degrees} = 2 \times \frac{\pi}{180} = 0.0349066 \, \text{radians} \)
- Convert \( L \) to m: \( 1 \, \text{m} = 1 \, \text{m} \)
- Shear strain: \( \gamma_{\text{max}} = \frac{\rho \phi}{L} = \frac{0.01 \times 0.0349066}{1} = 0.000349066 \)
The calculator returns:
- \( \gamma_{\text{max}} \): 0.0003

5. Frequently Asked Questions (FAQ)

Q: What is shear strain?
A: Shear strain (\( \gamma \)) is a measure of the deformation of a material due to shear stress, defined as the ratio of the displacement to the transverse dimension or the ratio of shear stress to shear modulus.

Q: How does shear strain differ from normal strain?
A: Normal strain measures deformation due to tensile or compressive forces (change in length over original length), while shear strain measures deformation due to shear forces (angular distortion).

Q: How is shear strain used in real life?
A: Shear strain is used in engineering to analyze how materials deform under shear forces, ensuring the stability and safety of structures like beams, shafts, and fasteners in applications such as bridges, buildings, and machinery.