Series Inductors Calculator

Inductor 1 (\( L_1 \)):

Inductor 2 (\( L_2 \)):

1. What is Series Inductors Calculator?

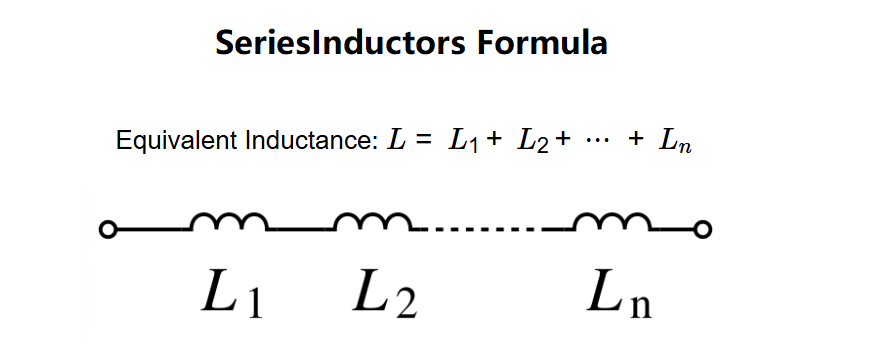
Definition: This calculator computes the equivalent inductance (\( L \)) of multiple inductors connected in series.

Purpose: It is used in electrical engineering to determine the total inductance of a series combination of inductors, which is essential for designing circuits such as filters, oscillators, and power supplies.

2. How Does the Calculator Work?

The calculator uses the following formula:

Equivalent Inductance: \( L = L_1 + L_2 + \cdots + L_n \)

Where:

\( L \): Equivalent inductance (H)
\( L_1, L_2, \ldots, L_n \): Inductances of the individual inductors (H)

Steps:

Enter the inductance values of the inductors (\( L_1, L_2, \ldots, L_n \)) with their units.
Add or remove inductor fields as needed (minimum of 2 inductors).
Convert all inputs to base units (H).
Calculate the equivalent inductance by summing the individual inductances.
Convert the result to the selected output unit (H, mH, µH).
Display the result: if the value is less than 0.001 in the selected unit, use scientific notation; otherwise, display with 4 decimal places.

3. Importance of Series Inductors Calculation

Calculating the equivalent inductance of inductors in series is crucial for:

Circuit Design: Determining the total inductance in a circuit with series inductors, which affects the circuit's behavior in applications like filters and resonant circuits.
Energy Storage: Understanding the combined inductance helps in calculating the total energy stored in the magnetic field of the inductors.
Impedance Matching: Adjusting the inductance in a circuit to match the impedance for optimal performance in RF and audio applications.

4. Using the Calculator

Example 1: Calculate the equivalent inductance of three inductors in series with \( L_1 = 5 \, \text{H} \), \( L_2 = 10 \, \text{H} \), and \( L_3 = 15 \, \text{H} \):

Inductor 1 (\( L_1 \)): 5 H
Inductor 2 (\( L_2 \)): 10 H
Inductor 3 (\( L_3 \)): 15 H
Equivalent Inductance (\( L \)): \( 5 + 10 + 15 = 30 \, \text{H} \)
Result: \( L = 30.0000 \, \text{H} \)

Example 2 (Demonstrating Scientific Notation): Calculate the equivalent inductance of two inductors in series with \( L_1 = 1 \, \text{µH} \) and \( L_2 = 2 \, \text{µH} \):

Inductor 1 (\( L_1 \)): 1 µH = \( 1 \times 10^{-6} \) H
Inductor 2 (\( L_2 \)): 2 µH = \( 2 \times 10^{-6} \) H
Equivalent Inductance (\( L \)): \( 1 \times 10^{-6} + 2 \times 10^{-6} = 3 \times 10^{-6} \, \text{H} \), in µH: \( 3 \times 10^{-6} \times 10^6 = 3 \, \text{µH} \)
Result: \( L = 3.0000 \, \text{µH} \)

5. Frequently Asked Questions (FAQ)

Q: What is the equivalent inductance of inductors in series?
A: The equivalent inductance of inductors in series is the sum of the individual inductances: \( L = L_1 + L_2 + \cdots + L_n \). This means the total inductance increases as more inductors are added in series.

Q: Why does the equivalent inductance increase in a series connection?
A: In a series connection, the same current flows through each inductor, and the total magnetic flux linkage is the sum of the flux linkages of each inductor. This results in a higher total inductance.

Q: Can I use this calculator for inductors with different units?
A: Yes, the calculator allows you to specify the unit (H, mH, µH) for each inductor. It converts all values to henries (H) for calculation and then converts the result to the selected output unit.