1. What is Section Modulus Calculator?
Definition: This calculator computes the elastic section modulus (\( S_x \), \( S_y \)) of various cross-sectional shapes, along with the moments of inertia (\( I_x \), \( I_y \)) and the distances from the centroid to the extreme fibers (\( y_c \), \( x_c \)).
Purpose: It is used in structural engineering to determine the bending strength of beams and other structural elements, helping to design safe and efficient structures.
2. How Does the Calculator Work?
The calculator uses the following formulas for each shape:
Formulas:
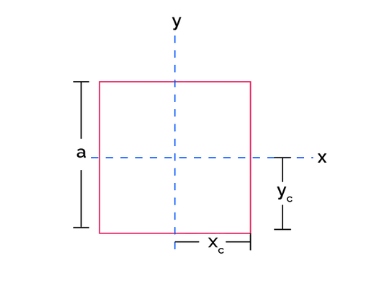
- Square (side length \( a \)):
- \( y_c = x_c = a/2 \)
- \( I_x = I_y = \frac{a^4}{12} \)
- \( S_x = S_y = \frac{I_x}{y_c} = \frac{a^3}{6} \)
- Rectangle (width \( b \), depth \( d \)):
- \( y_c = d/2 \)
- \( x_c = b/2 \)
- \( I_x = \frac{b d^3}{12} \)
- \( I_y = \frac{d b^3}{12} \)
- \( S_x = \frac{I_x}{y_c} = \frac{b d^2}{6} \)
- \( S_y = \frac{I_y}{x_c} = \frac{d b^2}{6} \)
- Hollow Rectangle (outer width \( b \), outer depth \( d \), inner width \( b_i \), inner depth \( d_i \)):
- \( y_c = d/2 \)
- \( x_c = b/2 \)
- \( I_x = \frac{b d^3 - b_i d_i^3}{12} \)
- \( I_y = \frac{d b^3 - d_i b_i^3}{12} \)
- \( S_x = \frac{I_x}{y_c} \)
- \( S_y = \frac{I_y}{x_c} \)
- Tee Section (flange width \( b \), flange thickness \( t \), web depth \( d \), web thickness \( t_w \)):
- \( A = t b + t_w d \)
- \( y_c = \frac{b t^2 + t_w d (2t + d)}{2 (t b + t_w d)} \)
- \( x_c = b/2 \)
- \( I_x = \frac{b (d + t)^3 - b^3 (b - t_w)}{3} - A (d + t - y_c)^2 \)
- \( I_y = \frac{t b^3 + d t_w^3}{12} \)
- \( S_x = \frac{I_x}{d + t - y_c} \)
- \( S_y = \frac{I_y}{x_c} \)
- Channel Section (flange width \( b \), flange thickness \( t \), web depth \( d \), web thickness \( t_w \)):
- \( A = t b + 2 t_w d \)
- \( y_c = \frac{(d + t) b^2 t + 2 t_w d (b - t_w)}{2 (b t + 2 t_w d)} \)
- \( x_c = b/2 \)
- \( I_x = \frac{b (d + t)^3 - (b - t_w) d^3}{12} - A (d + t - y_c)^2 \)
- \( I_y = \frac{(d + t) b^3 - d (b - 2 t_w)^3}{12} \)
- \( S_x = \frac{I_x}{d + t - y_c} \)
- \( S_y = \frac{I_y}{x_c} \)
- Wide-Flange Beam (Equal Flanges) (flange width \( b \), flange thickness \( t \), web depth \( d \), web thickness \( t_w \)):
- \( y_c = d/2 + t \)
- \( x_c = b/2 \)
- \( I_x = \frac{b (d + 2t)^3 - (b - t_w) d^3}{12} \)
- \( I_y = \frac{b t^3 + d t_w^3}{12} \)
- \( S_x = \frac{I_x}{y_c} \)
- \( S_y = \frac{I_y}{x_c} \)
- Angle (leg width \( b \), leg depth \( d \), thickness \( t \)):
- \( A = t (b + d - t) \)
- \( y_c = \frac{b^2 t + (d - t) t (b + t)}{2 (b t + d t - t^2)} \)
- \( x_c = \frac{b t (b - t) + d t (b + t)}{2 (b t + d t - t^2)} \)
- \( I_x = \frac{b d^3 - (b - t) (d - t)^3}{3} - A (d - y_c)^2 \)
- \( I_y = \frac{d b^3 - (d - t) (b - t)^3}{3} - A (b - x_c)^2 \)
- \( S_x = \frac{I_x}{d - y_c} \)
- \( S_y = \frac{I_y}{b - x_c} \)
- Circle (radius \( R \)):
- \( y_c = x_c = R \)
- \( I_x = I_y = \frac{\pi R^4}{4} \)
- \( S_x = S_y = \frac{I_x}{y_c} = \frac{\pi R^3}{4} \)
- Hollow Circle (outer radius \( R \), inner radius \( R_i \)):
- \( y_c = x_c = R \)
- \( I_x = I_y = \frac{\pi (R^4 - R_i^4)}{4} \)
- \( S_x = S_y = \frac{I_x}{y_c} \)
Unit Conversions:
- Dimensions (\( a \), \( b \), \( d \), \( b_i \), \( d_i \), \( t \), \( t_w \), \( R \), \( R_i \), \( y_c \), \( x_c \)):
- 1 mm = 1 mm
- 1 cm = 0.01 m
- 1 m = 1 m
- 1 in = 0.0254 m
- 1 ft = 0.3048 m
- Moment of Inertia (\( I_x \), \( I_y \)):
- 1 mm⁴ = 1 mm⁴
- 1 cm⁴ = 10⁻⁸ m⁴
- 1 m⁴ = 1 m⁴
- 1 in⁴ = (0.0254)⁴ m⁴
- Section Modulus (\( S_x \), \( S_y \)):
- 1 mm³ = 1 mm³
- 1 cm³ = 10⁻⁶ m³
- 1 m³ = 1 m³
- 1 in³ = (0.0254)³ m³
Steps:
- Select the cross-sectional shape (Square, Rectangle, Hollow Rectangle, Tee Section, Channel Section, Wide-Flange Beam, Angle, Circle, or Hollow Circle).
- Enter the dimensions of the shape with their respective units (e.g., \( a \), \( b \), \( d \), etc.).
- Convert all dimensions to meters for calculation.
- Calculate the distances from the centroid (\( y_c \), \( x_c \)), moments of inertia (\( I_x \), \( I_y \)), and section moduli (\( S_x \), \( S_y \)) using the appropriate formulas.
- Convert the results to the selected units for display.
- Display the results with 4 decimal places.
3. Importance of Section Modulus Calculation
Calculating the section modulus is crucial for:
- Structural Design: Determining the bending strength of beams and other structural elements to ensure they can withstand applied loads without excessive deflection or failure.
- Material Selection: Selecting appropriate cross-sectional shapes and sizes for specific applications based on their bending resistance.
- Safety Analysis: Ensuring that structural components meet safety standards by evaluating their capacity to resist bending stresses.
4. Using the Calculator
Example:
Calculate the section modulus for a rectangular cross-section with width \( b = 100 \, \text{mm} \) and depth \( d = 200 \, \text{mm} \).
- Select the shape as Rectangle.
- Enter the width, \( b = 100 \, \text{mm} \), and depth, \( d = 200 \, \text{mm} \).
- The calculator computes:
- Convert to meters: \( b = 0.1 \, \text{m} \), \( d = 0.2 \, \text{m} \).
- \( y_c = d/2 = 0.2/2 = 0.1 \, \text{m} = 100 \, \text{mm} \)
- \( x_c = b/2 = 0.1/2 = 0.05 \, \text{m} = 50 \, \text{mm} \)
- \( I_x = \frac{b d^3}{12} = \frac{0.1 \times (0.2)^3}{12} = 6.6667 \times 10^{-5} \, \text{m}^4 = 66667 \, \text{mm}^4 \)
- \( I_y = \frac{d b^3}{12} = \frac{0.2 \times (0.1)^3}{12} = 1.6667 \times 10^{-5} \, \text{m}^4 = 16667 \, \text{mm}^4 \)
- \( S_x = \frac{I_x}{y_c} = \frac{6.6667 \times 10^{-5}}{0.1} = 6.6667 \times 10^{-4} \, \text{m}^3 = 666.67 \, \text{mm}^3 \)
- \( S_y = \frac{I_y}{x_c} = \frac{1.6667 \times 10^{-5}}{0.05} = 3.3333 \times 10^{-4} \, \text{m}^3 = 333.33 \, \text{mm}^3 \)
5. Frequently Asked Questions (FAQ)
Q: What is the section modulus?
A: The section modulus (\( S_x \), \( S_y \)) is a geometric property of a cross-section that quantifies its resistance to bending. It is defined as the moment of inertia (\( I \)) divided by the distance from the centroid to the extreme fiber (\( y_c \), \( x_c \)).
Q: Why is the section modulus important in structural engineering?
A: The section modulus is critical for determining the bending strength of a structural element. It helps engineers design beams and other components to withstand bending stresses without failing or deforming excessively.
Q: How does the calculator handle different units?
A: The calculator allows users to input dimensions in various units (mm, cm, m, in, ft) and select output units for each parameter (\( y_c \), \( x_c \), \( I_x \), \( I_y \), \( S_x \), \( S_y \)). All calculations are performed in base units (meters, m⁴, m³), and the results are converted to the selected units for display.
Section Modulus Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back