Sag in a Transmission Line Calculator

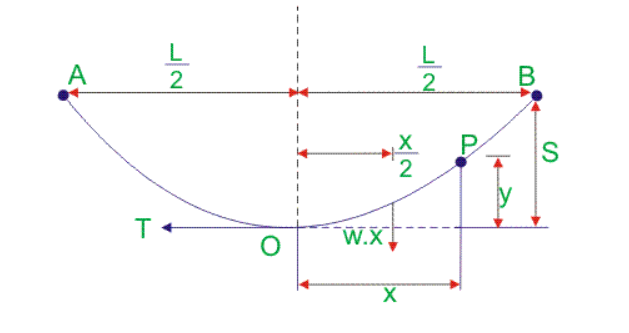
1. What is Sag in a Transmission Line Calculator?

Definition: This calculator computes the sag and working tension in a transmission line based on the span length, weight per unit length, horizontal tension, and safety factor, supporting both equal and unequal level supports.

Purpose: It is used in electrical engineering to design and analyze overhead power lines, ensuring proper clearance and structural integrity under varying support conditions, with a safety margin applied to the tension.

2. How Does the Calculator Work?

The calculator uses the following formulas based on the selected calculation type:

Common Formula:

Working Tension: \[ T_{\text{work}} = \frac{T}{\text{Safety Factor}} \]

Formulas for Equal Levels:

Sag: \[ S = \frac{w \cdot L^2}{8 \cdot T_{\text{work}}} \]

Formulas for Unequal Levels:

Sag at Support A: \[ S_1 = \frac{w \cdot x_1^2}{2 \cdot T_{\text{work}}} \]
Sag at Support B: \[ S_2 = \frac{w \cdot x_2^2}{2 \cdot T_{\text{work}}} \]
Span Length: \[ x_1 + x_2 = L \]
Height Difference: \[ S_2 - S_1 = h \]
Derived Equation: \[ S_2 - S_1 = \frac{w \cdot L}{2 \cdot T_{\text{work}}} (x_2 - x_1) \]
Solving for \( x_1 \): \[ x_1 = \frac{L}{2} - \frac{T_{\text{work}} \cdot h}{w \cdot L} \]
Solving for \( x_2 \): \[ x_2 = \frac{L}{2} + \frac{T_{\text{work}} \cdot h}{w \cdot L} \]

Where:

\( S \), \( S_1 \), \( S_2 \): Sag of the transmission line (m, ft, in)
\( w \): Weight per unit length (kg/m, lb/ft)
\( L \): Span length (m, ft, in)
\( T \): Horizontal tension (kg, lb)
\( T_{\text{work}} \): Working tension after applying safety factor (kg, lb)
\( \text{Safety Factor} \): Divisor for tension to ensure safety (default = 2)
\( h \): Height difference between supports (m, ft, in)
\( x_1 \), \( x_2 \): Horizontal distances from the lowest point to supports A and B (m)

Unit Conversions:

Length (\( L \), \( h \)):
- 1 m = 1 m
- 1 ft = 0.3048 m
- 1 in = 0.0254 m
Weight per Unit Length (\( w \)):
- 1 kg/m = 1 kg/m
- 1 lb/ft = 1.48816 kg/m (0.453592 kg / 0.3048 m)
Tension (\( T \), \( T_{\text{work}} \)):
- 1 kg = 9.81 N
- 1 lb = 4.44822 N
Sag (\( S \), \( S_1 \), \( S_2 \)):
- 1 m = 1 m
- 1 ft = 0.3048 m
- 1 in = 0.0254 m

Steps:

Select the calculation type (Equal Levels or Unequal Levels).
Enter the span length (\( L \)), weight per unit length (\( w \)), and horizontal tension (\( T \)) with their respective units (tension defaults to kg).
Enter the safety factor (default is 2).
If Unequal Levels is selected, enter the height difference (\( h \)) between supports.
Convert all inputs to base units (m for length, kg/m for weight, N for tension).
Calculate the working tension: \( T_{\text{work}} = \frac{T}{\text{Safety Factor}} \).
Calculate the sag(s) based on the selected type:
- For Equal Levels: Use \( S = \frac{w \cdot L^2}{8 \cdot T_{\text{work}}} \).
- For Unequal Levels: Solve for \( x_1 \) and \( x_2 \), then compute \( S_1 \) and \( S_2 \).
Convert the sag(s) to the selected unit for display.
Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Sag Calculation

Calculating the sag in a transmission line is crucial for:

Safety: Ensuring proper clearance between the transmission line and the ground or other structures, especially with varying support heights, while accounting for a safety margin.
Structural Integrity: Using a reduced working tension to simulate safer operating conditions, preventing excessive sag that could strain the line or towers.
Efficiency: Optimizing the design of power lines for cost-effective and reliable operation under different terrain conditions.

4. Using the Calculator

Example 1 (Equal Levels): Calculate the sag of a transmission line with a span length of 100 m, a weight per unit length of 1 kg/m, a horizontal tension of 500 kg, and a safety factor of 2.

Select "Supports at Equal Levels."
Enter the span length as 100 m.
Enter the weight per unit length as 1 kg/m.
Enter the horizontal tension as 500 kg.
Enter the safety factor as 2.
Convert tension: \( 500 \, \text{kg} \times 9.81 = 4905 \, \text{N} \).
Calculate working tension: \( T_{\text{work}} = \frac{4905}{2} = 2452.5 \, \text{N} \) (displayed as \( \frac{2452.5}{9.81} \approx 250.0 \, \text{kg} \)).
The calculator returns the sag as 0.5097 m:
- Sag = \( \frac{w \cdot L^2}{8 \cdot T_{\text{work}}} \)
- = \( \frac{1 \cdot 100^2}{8 \cdot 2452.5} \)
- = \( \frac{10000}{19620} \approx 0.5097 \) m

Example 2 (Unequal Levels): Calculate the sag of a transmission line with a span length of 100 m, a weight per unit length of 1 kg/m, a horizontal tension of 500 kg, a safety factor of 2, and a height difference of 0.5 m between supports.

Select "Supports at Unequal Levels."
Enter the span length as 100 m.
Enter the weight per unit length as 1 kg/m.
Enter the horizontal tension as 500 kg.
Enter the safety factor as 2.
Enter the height difference as 0.5 m.
Convert tension: \( 500 \, \text{kg} \times 9.81 = 4905 \, \text{N} \).
Calculate working tension: \( T_{\text{work}} = \frac{4905}{2} = 2452.5 \, \text{N} \) (displayed as \( \frac{2452.5}{9.81} \approx 250.0 \, \text{kg} \)).
Calculate \( x_1 \) and \( x_2 \):
- \( x_1 = \frac{L}{2} - \frac{T_{\text{work}} \cdot h}{w \cdot L} \)
- = \( \frac{100}{2} - \frac{2452.5 \cdot 0.5}{1 \cdot 100} \)
- = \( 50 - 12.2625 = 37.7375 \) m
- \( x_2 = 100 - 37.7375 = 62.2625 \) m
Calculate \( S_1 \):
- \( S_1 = \frac{w \cdot x_1^2}{2 \cdot T_{\text{work}}} \)
- = \( \frac{1 \cdot 37.7375^2}{2 \cdot 2452.5} \)
- = \( \frac{1424.1189}{4905} \approx 0.2903 \) m
Calculate \( S_2 \):
- \( S_2 = \frac{w \cdot x_2^2}{2 \cdot T_{\text{work}}} \)
- = \( \frac{1 \cdot 62.2625^2}{2 \cdot 2452.5} \)
- = \( \frac{3876.6191}{4905} \approx 0.7903 \) m

5. Frequently Asked Questions (FAQ)

Q: What is working tension?
A: Working tension (\( T_{\text{work}} \)) is the tension divided by the safety factor, used in sag calculations to simulate safer operating conditions.

Q: Why is a safety factor used?
A: The safety factor reduces the effective tension used in calculations, simulating a safer scenario by increasing the sag, which helps account for uncertainties like wind loads or temperature changes.

Q: How does the tension unit "kg" work?
A: The unit "kg" for tension is interpreted as a mass, converted to force in Newtons using \( 1 \, \text{kg} = 9.81 \, \text{N} \), as tension is a force measurement.

Reference

https://www.electrical4u.com/sag-in-overhead-conductor/

https://www.rcet.org.in/uploads/academics/rohini_43235565283.pdf