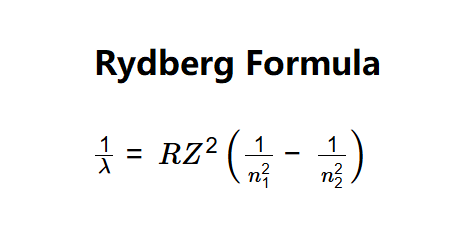Rydberg Equation Calculator

Wavelength (\( \lambda \)):

Frequency (\( f \)):

Energy (\( E \)):

1. What is the Rydberg Equation Calculator?

Definition: This calculator uses the Rydberg formula to compute the wavelength (\( \lambda \)), frequency (\( f \)), and energy (\( E \)) of the photon involved in an electron transition in a hydrogen-like atom, based on the atomic number (\( Z \)), initial principal quantum number (\( n_1 \)), and final principal quantum number (\( n_2 \)).

Purpose: It is used in atomic physics to predict the wavelengths of light involved in electron transitions in hydrogen-like atoms, which is fundamental for understanding atomic spectra and quantum mechanics, for both emission and absorption processes.

2. How Does the Calculator Work?

The calculator uses the following equations:

\( \frac{1}{\lambda} = R Z^2 \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right) \)
\( f = \frac{c}{|\lambda|} \)
\( E = h f \)

Where:

\( \lambda \): Wavelength (m, cm, mm, nm, pm, Å; negative for absorption);
\( f \): Frequency (Hz, kHz, MHz, GHz, THz);
\( E \): Energy (J, neV, µeV, meV, eV, keV, MeV);
\( Z \): Atomic number;
\( n_1 \), \( n_2 \): Initial and final principal quantum numbers;
\( R \): Rydberg constant (\( 1.0973 \times 10^7 \, \text{m}^{-1} \));
\( c \): Speed of light (\( 299,792,458 \, \text{m/s} \));
\( h \): Planck constant (\( 6.626 \times 10^{-34} \, \text{J·s} \)).

Steps:

Enter the atomic number (\( Z \)).
Enter the initial principal quantum number (\( n_1 \)).
Enter the final principal quantum number (\( n_2 \)).
Calculate the inverse wavelength: \( \frac{1}{\lambda} = R Z^2 \left( \frac{1}{n_1^2} - \frac{1}{n_2^2} \right) \).
Calculate the wavelength: \( \lambda = \frac{1}{\text{inverse wavelength}} \).
Calculate the frequency: \( f = \frac{c}{|\lambda|} \).
Calculate the energy: \( E = h f \).
Convert the results to the selected output units and display, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Rydberg Equation Calculation

Calculating the Rydberg equation parameters is crucial for:

Atomic Physics: Predicting the wavelengths of spectral lines in hydrogen-like atoms for both emission and absorption.
Spectroscopy: Analyzing the spectra of atoms to identify elements and study their energy levels.
Quantum Mechanics Education: Demonstrating the quantized nature of energy levels in atoms.

4. Using the Calculator

Example 1 (Emission): Calculate the emitted photon parameters for a hydrogen atom (\( Z = 1 \)) transitioning from \( n_1 = 2 \) to \( n_2 = 1 \) (Lyman-alpha line):

Atomic Number: \( Z = 1 \);
Initial Quantum Number: \( n_1 = 2 \);
Final Quantum Number: \( n_2 = 1 \);
Inverse Wavelength: \( \frac{1}{\lambda} = 1.0973 \times 10^7 \times 1^2 \times \left( \frac{1}{2^2} - \frac{1}{1^2} \right) = 1.0973 \times 10^7 \times \left( \frac{1}{4} - 1 \right) = 8.22975 \times 10^6 \, \text{m}^{-1} \);
Wavelength: \( \lambda = \frac{1}{8.22975 \times 10^6} \approx 1.215 \times 10^{-7} \, \text{m} \approx 121.5 \, \text{nm} \);
Frequency: \( f = \frac{299,792,458}{1.215 \times 10^{-7}} \approx 2.467 \times 10^{15} \, \text{Hz} \approx 2467 \, \text{THz} \);
Energy: \( E = 6.626 \times 10^{-34} \times 2.467 \times 10^{15} \approx 1.635 \times 10^{-18} \, \text{J} \approx 10.20 \, \text{eV} \);
Result: \( \lambda = 121.5000 \, \text{nm} \), \( f = 2467.0000 \, \text{THz} \), \( E = 10.2000 \, \text{eV} \).

Example 2 (Absorption): Calculate the absorbed photon parameters for a hydrogen atom (\( Z = 1 \)) transitioning from \( n_1 = 1 \) to \( n_2 = 2 \):

Atomic Number: \( Z = 1 \);
Initial Quantum Number: \( n_1 = 1 \);
Final Quantum Number: \( n_2 = 2 \);
Inverse Wavelength: \( \frac{1}{\lambda} = 1.0973 \times 10^7 \times 1^2 \times \left( \frac{1}{1^2} - \frac{1}{2^2} \right) = 1.0973 \times 10^7 \times \left( 1 - \frac{1}{4} \right) = -8.22975 \times 10^6 \, \text{m}^{-1} \);
Wavelength: \( \lambda = \frac{1}{-8.22975 \times 10^6} \approx -1.215 \times 10^{-7} \, \text{m} \approx -121.5 \, \text{nm} \);
Frequency: \( f = \frac{299,792,458}{| -1.215 \times 10^{-7} |} \approx 2.467 \times 10^{15} \, \text{Hz} \approx 2467 \, \text{THz} \);
Energy: \( E = 6.626 \times 10^{-34} \times 2.467 \times 10^{15} \approx 1.635 \times 10^{-18} \, \text{J} \approx 10.20 \, \text{eV} \);
Result: \( \lambda = -121.5000 \, \text{nm} \), \( f = 2467.0000 \, \text{THz} \), \( E = 10.2000 \, \text{eV} \).

5. Frequently Asked Questions (FAQ)

Q: What does the Rydberg formula tell us?
A: The Rydberg formula predicts the wavelength of light involved in an electron transition in a hydrogen-like atom, revealing the quantized nature of atomic energy states. A positive wavelength indicates emission (\( n_1 > n_2 \)), while a negative wavelength indicates absorption (\( n_1 < n_2 \)).

Q: What does a negative wavelength mean?
A: A negative wavelength indicates an absorption process, where the electron transitions from a lower energy level (\( n_1 \)) to a higher energy level (\( n_2 \)), absorbing a photon. The frequency and energy are still positive, as they represent the photon's properties.

Q: Can this calculator be used for multi-electron atoms?
A: This calculator is designed for hydrogen-like atoms (one electron). For multi-electron atoms, electron-electron interactions complicate the energy levels, requiring more advanced models.