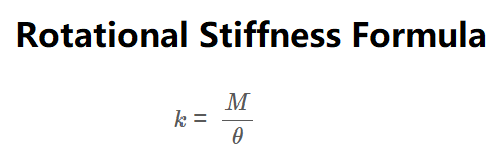Rotational Stiffness Calculator

1. What is a Rotational Stiffness Calculator?

Definition: This calculator computes the rotational stiffness (\( k \)) of an object, which is the ratio of the applied moment (\( M \)) to the angle of rotation (\( \theta \)).

Purpose: It is used in physics and engineering to quantify how resistant an object is to rotational deformation, which is crucial for designing systems like springs, shafts, and torsional elements.

2. How Does the Calculator Work?

The calculator uses the following formula:

Rotational Stiffness: \[ k = \frac{M}{\theta} \] Where:

\( k \): Rotational stiffness (N·m/rad, N·m/deg, lb·ft/rad, lb·ft/deg)
\( M \): Applied moment (N·m, N·cm, lb·ft)
\( \theta \): Angle of rotation (rad, deg)

Unit Conversions:

Applied Moment (\( M \)): N·m, N·cm (1 N·cm = 0.01 N·m), lb·ft (1 lb·ft = 1.355817948 N·m)
Angle of Rotation (\( \theta \)): rad, deg (1 deg = \( \frac{\pi}{180} \) rad)
Rotational Stiffness (\( k \)): N·m/rad, N·m/deg (1 rad = \( \frac{180}{\pi} \) deg), lb·ft/rad (1 N·m = 0.737562149 lb·ft), lb·ft/deg (combine conversions)

Steps:

Enter the applied moment and angle of rotation, and select their units.
Convert all inputs to base units (N·m for moment, rad for angle).
Calculate the rotational stiffness using the formula \( k = \frac{M}{\theta} \).
Convert the result to the selected stiffness unit.
Display the result, using scientific notation for values less than 0.001, otherwise with 3 decimal places.

3. Importance of Rotational Stiffness Calculation

Calculating rotational stiffness is crucial for:

Physics Education: Understanding the relationship between torque and angular displacement in rotational dynamics.
Engineering Design: Designing mechanical components like torsional springs, shafts, and beams that undergo rotational deformation.
Structural Analysis: Ensuring the stability and performance of structures under torsional loads.

4. Using the Calculator

Examples:

Example 1: For \( M = 100 \, \text{N·m} \), \( \theta = 0.5 \, \text{rad} \), stiffness in N·m/rad:
- Rotational Stiffness: \( k = \frac{100}{0.5} = 200 \, \text{N·m/rad} \)
Example 2: For \( M = 5000 \, \text{N·cm} \), \( \theta = 30 \, \text{deg} \), stiffness in lb·ft/deg:
- Convert: \( M = 5000 \times 0.01 = 50 \, \text{N·m} \), \( \theta = 30 \times \frac{\pi}{180} = 0.5236 \, \text{rad} \)
- Rotational Stiffness: \( k = \frac{50}{0.5236} = 95.493 \, \text{N·m/rad} \)
- Convert: \( 95.493 \times 0.737562149 = 70.428 \, \text{lb·ft/rad} \), then \( 70.428 \times \frac{180}{\pi} = 4035.996 \, \text{lb·ft/deg} \)

5. Frequently Asked Questions (FAQ)

Q: What is rotational stiffness?
A: Rotational stiffness is a measure of how resistant an object is to rotational deformation, defined as the ratio of the applied moment to the resulting angle of rotation.

Q: How does rotational stiffness differ from linear stiffness?
A: Rotational stiffness relates torque (moment) to angular displacement, while linear stiffness relates force to linear displacement. Rotational stiffness is relevant for systems undergoing torsion, such as shafts and springs.

Q: What are the units of rotational stiffness?
A: The base unit is \( \text{N·m/rad} \), but it can also be expressed in \( \text{N·m/deg} \), \( \text{lb·ft/rad} \), or \( \text{lb·ft/deg} \) depending on the units of moment and angle.