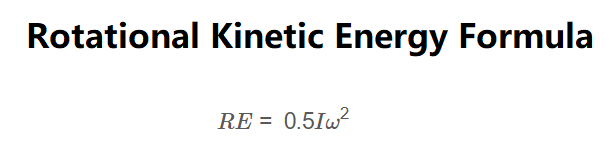Rotational Kinetic Energy Calculator

1. What is a Rotational Kinetic Energy Calculator?

Definition: This calculator computes the rotational kinetic energy (\( RE \)) of a rotating object based on its moment of inertia (\( I \)) and angular velocity (\( \omega \)).

Purpose: It is used in physics and engineering to quantify the energy associated with rotational motion, which is essential for analyzing systems like flywheels, turbines, and rotating machinery.

2. How Does the Calculator Work?

The calculator uses the following formula:

Rotational Kinetic Energy: \[ RE = 0.5 I \omega^2 \] Where:

\( RE \): Rotational kinetic energy (J, kJ, MJ, Wh)
\( I \): Moment of inertia (kg·m², kg·cm², g·cm²)
\( \omega \): Angular velocity (rad/s, Hz, RPM)

Unit Conversions:

Moment of Inertia (\( I \)): kg·m², kg·cm² (1 kg·m² = 10000 kg·cm²), g·cm² (1 kg·m² = 100000 g·cm²)
Angular Velocity (\( \omega \)): rad/s, Hz (1 Hz = \( 2\pi \) rad/s), RPM (1 RPM = \( \frac{2\pi}{60} \) rad/s)
Rotational Kinetic Energy (\( RE \)): J, kJ (1 kJ = 1000 J), MJ (1 MJ = 1000000 J), Wh (1 Wh = 3600 J)

Steps:

Enter the moment of inertia and angular velocity, and select their units.
Convert all inputs to base units (kg·m² for moment of inertia, rad/s for angular velocity).
Calculate the rotational kinetic energy using the formula \( RE = 0.5 I \omega^2 \).
Convert the result to the selected energy unit.
Display the result, using scientific notation for values less than 0.001, otherwise with 3 decimal places.

3. Importance of Rotational Kinetic Energy Calculation

Calculating rotational kinetic energy is crucial for:

Physics Education: Understanding the energy associated with rotational motion and its conservation.
Engineering Applications: Designing rotating systems like flywheels, motors, and turbines, where rotational energy storage is key.
Energy Analysis: Evaluating the efficiency and performance of mechanical systems involving rotation.

4. Using the Calculator

Examples:

Example 1: For \( I = 0.5 \, \text{kg·m}^2 \), \( \omega = 10 \, \text{rad/s} \), energy in J:
- Rotational Kinetic Energy: \( RE = 0.5 \times 0.5 \times (10)^2 = 0.5 \times 0.5 \times 100 = 25 \, \text{J} \)
Example 2: For \( I = 1000 \, \text{g·cm}^2 \), \( \omega = 60 \, \text{RPM} \), energy in kJ:
- Convert: \( I = 1000 \times 0.00001 = 0.01 \, \text{kg·m}^2 \), \( \omega = 60 \times \frac{2\pi}{60} = 2\pi \, \text{rad/s} \approx 6.2832 \, \text{rad/s} \)
- Rotational Kinetic Energy: \( RE = 0.5 \times 0.01 \times (6.2832)^2 = 0.5 \times 0.01 \times 39.4784 = 0.197392 \, \text{J} \)
- Convert: \( 0.197392 \times 0.001 = 0.000 \, \text{kJ} \) (displayed as \( 1.974 \times 10^{-4} \, \text{kJ} \))

5. Frequently Asked Questions (FAQ)

Q: What is rotational kinetic energy?
A: Rotational kinetic energy is the energy an object possesses due to its rotational motion, dependent on its moment of inertia and angular velocity.

Q: How is angular velocity related to frequency?
A: Angular velocity (\( \omega \)) in rad/s is related to frequency (\( f \)) in Hz by \( \omega = 2\pi f \), and to RPM by \( \omega = \frac{2\pi}{60} \times \text{RPM} \).

Q: Why is moment of inertia important in this calculation?
A: The moment of inertia (\( I \)) quantifies how the mass of an object is distributed relative to the axis of rotation, directly affecting the energy required for rotation.