Rod Diameter Calculator - Axial Load Effect

Initial Area (A):

Load (P):

Young's Modulus (E):

Poisson's Ratio (ν):

Unit Converter ▲

Unit Converter ▼

From:	To:

1. What is the Rod Diameter Calculator?

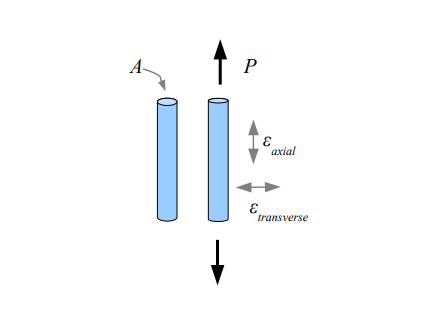
Definition: The Rod Diameter Calculator determines the initial and final diameter of a rod under an axial tensile load, including the change in diameter, accounting for axial and transverse strain using Poisson's ratio.

Purpose: Helps engineers analyze dimensional changes in rods due to loading.

Reference:Applied Strength of Materials for Engineering Technology

http://www.etcs.pfw.edu/~dupenb/ET_200/Applied%20Str%20of%20Mat%20for%20ET%20v14%20July%202018.pdf

2. How Does the Calculator Work?

Formula:

\( A = \frac{\pi d^2}{4} \), \( \epsilon_{long} = \frac{P}{A \cdot E} \), \( \epsilon_{transverse} = -\nu \cdot \epsilon_{long} \), \( \delta_{transverse} = \epsilon_{transverse} \cdot d_i \), \( d_f = d_i + \delta_{transverse} \)

Where:

\(A\): Cross-sectional area (in²)
\(d_i\): Initial diameter (in)
\(P\): Load (lb)
\(E\): Young's modulus (psi)
\(\nu\): Poisson's ratio
\(\epsilon_{long}\): Axial strain
\(\epsilon_{transverse}\): Transverse strain
\(\delta_{transverse}\): Change in diameter (in)
\(d_f\): Final diameter (in)

Steps:

Step 1: Input Initial Area. Enter the cross-sectional area (e.g., 0.19635 in²).
Step 2: Input Load. Enter the axial load (e.g., 6000 lb).
Step 3: Input Young's Modulus. Enter the material's modulus (e.g., 10×10⁶ psi).
Step 4: Select or Input Poisson's Ratio. Choose a material (Steel: 0.25, Aluminum: 0.33, Concrete: 0.10-0.20 avg 0.15) or enter a custom value.
Step 5: Calculate. The calculator computes initial diameter, change in diameter, and final diameter in both inches and centimeters.

3. Importance of Diameter Calculation

Calculating diameter changes is crucial for:

Material Deformation: Ensures the rod's dimensional stability under load.
Design Safety: Helps determine if the rod meets design specifications.
Unit Consistency: Supports conversions across units.

4. Using the Calculator

Example: Area = 0.19635 in², Load = 6000 lb, Young's Modulus = 10×10⁶ psi, Poisson's Ratio = 0.33 (Aluminum):

Step 1: \( d_i = \sqrt{\frac{4 \cdot 0.19635}{\pi}} \approx 0.50000 \, \text{in} = 1.27000 \, \text{cm} \).
Step 2: \( \epsilon_{long} = \frac{6000}{0.19635 \cdot 10^7} \approx 0.000306 \).
Step 3: \( \epsilon_{transverse} = -0.33 \cdot 0.000306 \approx -0.00101 \).
Step 4: \( \delta_{transverse} = -0.00101 \cdot 0.50000 \approx -0.000504 \, \text{in} = -0.001280 \, \text{cm} \).
Step 5: \( d_f = 0.50000 - 0.000504 \approx 0.49950 \, \text{in} = 1.26881 \, \text{cm} \).

5. Frequently Asked Questions (FAQ)

Q: What is Poisson's ratio?
A: Poisson's ratio is the ratio of transverse strain to axial strain under elastic deformation.

Q: Can I use metric units?
A: Yes, the calculator converts mm² and kN to in² and lb internally, and displays diameters in both in and cm.

Q: Is this accurate for all materials?
A: Yes, if material properties (E, ν) are correctly input.