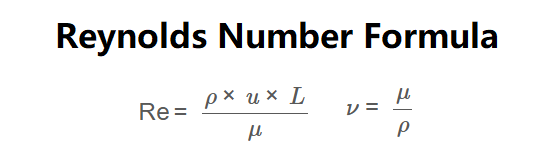1. What is Reynolds Number Calculator?
Definition: This calculator computes the kinematic viscosity (\( \nu \)) and Reynolds number (\( \text{Re} \)) of a fluid flow, based on the fluid density (\( \rho \)), dynamic viscosity (\( \mu \)), velocity (\( u \)), and characteristic length (\( L \)).
Purpose: It is used in fluid dynamics to determine the flow regime (laminar, transitional, or turbulent), aiding in the design of pipes, aircraft, and other systems involving fluid flow.
2. How Does the Calculator Work?
The calculator uses the following formulas:
Formulas:
\[
\nu = \frac{\mu}{\rho}
\]
\[
\text{Re} = \frac{\rho \times u \times L}{\mu}
\]
\[
\text{Re} = \frac{u \times L}{\nu}
\]
Where:
- \( \text{Re} \): Reynolds number (dimensionless)
- \( \rho \): Fluid density (kg/m³, lb/ft³)
- \( u \): Velocity (m/s, ft/s, km/h, mph)
- \( L \): Characteristic length (m, cm, mm, in, ft)
- \( \mu \): Dynamic viscosity (Pa·s, cP)
- \( \nu \): Kinematic viscosity (m²/s, ft²/s)
Predefined Fluid Data:
- Air (15 °C): \( \rho = 1.225 \, \text{kg/m³} \), \( \mu = 1.81 \times 10^{-5} \, \text{Pa·s} \)
- Air (25 °C): \( \rho = 1.184 \, \text{kg/m³} \), \( \mu = 1.85 \times 10^{-5} \, \text{Pa·s} \)
- Water (10 °C): \( \rho = 999.7 \, \text{kg/m³} \), \( \mu = 1.31 \times 10^{-3} \, \text{Pa·s} \)
- Water (50 °C): \( \rho = 988 \, \text{kg/m³} \), \( \mu = 5.47 \times 10^{-4} \, \text{Pa·s} \)
- Water (90 °C): \( \rho = 965 \, \text{kg/m³} \), \( \mu = 3.15 \times 10^{-4} \, \text{Pa·s} \)
- Blood (37 °C): \( \rho = 1060 \, \text{kg/m³} \), \( \mu = 3.75 \times 10^{-3} \, \text{Pa·s} \) (average of 3.5 to 4 × 10⁻³)
- Honey: \( \rho = 1450 \, \text{kg/m³} \), \( \mu = 6 \, \text{Pa·s} \)
- Peanut Butter: \( \rho = 1082 \, \text{kg/m³} \), \( \mu = 0.25 \, \text{Pa·s} \)
- Acetone (25 °C): \( \rho = 791 \, \text{kg/m³} \), \( \mu = 3.06 \times 10^{-4} \, \text{Pa·s} \)
- Ethanol (25 °C): \( \rho = 789 \, \text{kg/m³} \), \( \mu = 1.074 \times 10^{-3} \, \text{Pa·s} \)
- Mercury (25 °C): \( \rho = 13594 \, \text{kg/m³} \), \( \mu = 1.526 \times 10^{-3} \, \text{Pa·s} \)
- Liquid Nitrogen (-196 °C): \( \rho = 807 \, \text{kg/m³} \), \( \mu = 1.58 \times 10^{-4} \, \text{Pa·s} \)
- Olive Oil (25 °C): \( \rho = 920 \, \text{kg/m³} \), \( \mu = 0.081 \, \text{Pa·s} \)
Unit Conversions:
- Density (\( \rho \)):
- 1 kg/m³ = 1 kg/m³
- 1 lb/ft³ = 16.0185 kg/m³
- Dynamic Viscosity (\( \mu \)):
- 1 Pa·s = 1 Pa·s
- 1 cP = 0.001 Pa·s
- Velocity (\( u \)):
- 1 m/s = 1 m/s
- 1 ft/s = 0.3048 m/s
- 1 km/h = 0.277778 m/s
- 1 mph = 0.44704 m/s
- Characteristic Length (\( L \)):
- 1 m = 1 m
- 1 cm = 0.01 m
- 1 mm = 0.001 m
- 1 in = 0.0254 m
- 1 ft = 0.3048 m
- Kinematic Viscosity (\( \nu \)):
- 1 m²/s = 1 m²/s
- 1 ft²/s = \( (0.3048)^2 \) m²/s
Steps:
- Select a fluid from the dropdown or choose "Custom" to enter your own values.
- If a predefined fluid is selected, the fields for density and dynamic viscosity will auto-fill with units forced to kg/m³ for density and Pa·s for dynamic viscosity, as shown in the image, and become read-only.
- Enter the fluid density (\( \rho \)) with its respective unit (kg/m³, lb/ft³) if using a custom fluid.
- Enter the dynamic viscosity (\( \mu \)) with its respective unit (Pa·s, cP) if using a custom fluid.
- Enter the velocity (\( u \)) with its respective unit (m/s, ft/s, km/h, mph).
- Enter the characteristic length (\( L \)) with its respective unit (m, cm, mm, in, ft).
- Convert all inputs to SI units (kg/m³ for \( \rho \), Pa·s for \( \mu \), m/s for \( u \), m for \( L \)).
- Calculate the kinematic viscosity (\( \nu \)) and Reynolds number (\( \text{Re} \)) using the formulas.
- Convert the kinematic viscosity to the selected unit and display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.
3. Importance of Reynolds Number Calculation
Calculating the Reynolds number is crucial for:
- Flow Regime Determination: Determining whether the flow is laminar (\( \text{Re} < 2300 \)), transitional (\( 2300 \leq \text{Re} \leq 4000 \)), or turbulent (\( \text{Re} > 4000 \)) in pipes, or other thresholds in different geometries.
- System Design: Designing pipes, ducts, and aerodynamic structures to optimize fluid flow and minimize energy losses.
- Engineering Applications: Analyzing fluid behavior in applications like HVAC systems, aircraft design, and biomedical engineering (e.g., blood flow).
4. Using the Calculator
Examples:
- Example 1: Calculate the kinematic viscosity and Reynolds number for Blood at 37 °C flowing at 2 m/s through a vessel with a characteristic length of 0.05 m, with kinematic viscosity in m²/s:
- Select "Blood (37 °C)" (auto-fills: \( \rho = 1060 \, \text{kg/m³} \), \( \mu = 0.00375 \, \text{Pa·s} \)).
- Enter \( u = 2 \) m/s.
- Enter \( L = 0.05 \) m.
- Kinematic viscosity: \( \nu = \frac{0.00375}{1060} = 3.5377 \times 10^{-6} \, \text{m²/s} \)
- Reynolds number: \( \text{Re} = \frac{1060 \times 2 \times 0.05}{0.00375} = 28266 \)
- Result: \( \nu = 3.5377 \times 10^{-6} \, \text{m²/s} \), \( \text{Re} = 28266 \)
- Example 2: Calculate the kinematic viscosity and Reynolds number for a custom fluid with density 1200 kg/m³, dynamic viscosity 0.01 Pa·s, velocity 10 ft/s, and characteristic length 1 in, with kinematic viscosity in ft²/s:
- Select "Custom".
- Enter \( \rho = 1200 \) kg/m³.
- Enter \( \mu = 0.01 \) Pa·s.
- Enter \( u = 10 \) ft/s.
- Convert to m/s: \( u = 10 \times 0.3048 = 3.048 \, \text{m/s} \)
- Enter \( L = 1 \) in.
- Convert to m: \( L = 1 \times 0.0254 = 0.0254 \, \text{m} \)
- Kinematic viscosity: \( \nu = \frac{0.01}{1200} = 8.3333 \times 10^{-6} \, \text{m²/s} \)
- Convert to ft²/s: \( \nu = 8.3333 \times 10^{-6} \div (0.3048)^2 = 8.9699 \times 10^{-5} \, \text{ft²/s} \)
- Reynolds number: \( \text{Re} = \frac{1200 \times 3.048 \times 0.0254}{0.01} = 9287 \)
- Result: \( \nu = 8.9699 \times 10^{-5} \, \text{ft²/s} \), \( \text{Re} = 9287 \)
5. Frequently Asked Questions (FAQ)
Q: What does the Reynolds number indicate?
A: The Reynolds number indicates the flow regime: laminar (\( \text{Re} < 2300 \)), transitional (\( 2300 \leq \text{Re} \leq 4000 \)), or turbulent (\( \text{Re} > 4000 \)) for pipe flow, helping predict flow behavior.
Q: What is the characteristic length (\( L \))?
A: The characteristic length (\( L \)) is a dimension that represents the geometry of the flow, such as the diameter of a pipe, the length of a plate, or the chord of an airfoil.
Q: Why are predefined fluid values provided?
A: Predefined fluid values simplify calculations by providing typical properties for common fluids at specific temperatures, allowing users to quickly compute values without needing to look up data.
Reynolds Number Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back