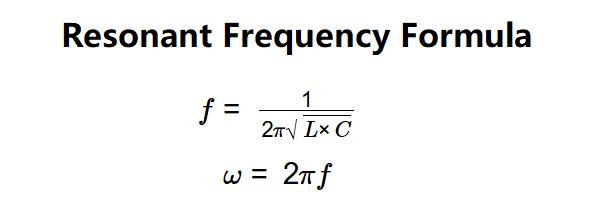Resonant Frequency Calculator for LC Circuits

Inductance (\( L \)):

Capacitance (\( C \)):

Resonant Frequency (\( f \)):

Angular Frequency (\( \omega \)):

1. What is Resonant Frequency Calculator for LC Circuits?

Definition: This calculator computes the resonant frequency (\( f \)) and angular frequency (\( \omega \)) of an LC circuit, which consists of an inductor (\( L \)) and a capacitor (\( C \)) in series or parallel.

Purpose: It is used in electronics to determine the natural frequency at which an LC circuit oscillates, which is essential for designing filters, oscillators, and tuning circuits in radios and other RF applications.

2. How Does the Calculator Work?

The calculator uses the following formulas for an LC circuit:

\( f = \frac{1}{2 \pi \sqrt{L \times C}} \)
\( \omega = 2 \pi f \)

Where:

\( f \): Resonant frequency (Hz);
\( \omega \): Angular frequency (rad/s);
\( L \): Inductance (H);
\( C \): Capacitance (F).

Steps:

Enter the inductance (\( L \)) and capacitance (\( C \)) with their units.
Convert inductance to Henries and capacitance to Farads.
Calculate the resonant frequency using the formula above.
Calculate the angular frequency using \( \omega = 2 \pi f \).
Convert the frequency and angular frequency to the selected output units (Hz/kHz/MHz for frequency, rad/s/krad/s/Mrad/s for angular frequency).
Display results in scientific notation if their absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Resonant Frequency Calculation

Calculating the resonant frequency of an LC circuit is crucial for:

Signal Processing: Designing bandpass filters and oscillators used in radios, amplifiers, and tuners to select specific frequencies.
RF Applications: Tuning circuits in transmitters and receivers to match the frequency of incoming signals, ensuring clear communication.
Circuit Design: Ensuring that LC circuits operate at their natural frequency for maximum efficiency and performance.

4. Using the Calculator

Example 1: Calculate the resonant frequency and angular frequency for an LC circuit with \( L = 1 \, \text{mH} \) and \( C = 220 \, \text{pF} \):

Input Values:
\( L = 1 \, \text{mH} = 1 \times 10^{-3} \, \text{H} \);
\( C = 220 \, \text{pF} = 220 \times 10^{-12} = 2.2 \times 10^{-10} \, \text{F} \);
LC Product: \( L \times C = (1 \times 10^{-3}) \times (2.2 \times 10^{-10}) = 2.2 \times 10^{-13} \);
Resonant Frequency: \( f = \frac{1}{2 \pi \sqrt{L \times C}} = \frac{1}{2 \pi \sqrt{2.2 \times 10^{-13}}} \approx 339319 \, \text{Hz} = 339.319 \, \text{kHz} \);
Angular Frequency: \( \omega = 2 \pi f = 2 \pi \times 339319 \approx 2132000 \, \text{rad/s} = 2.132 \, \text{Mrad/s} \);
Result: \( f = 339.3190 \, \text{kHz} \), \( \omega = 2.1320 \, \text{Mrad/s} \).

Example 2: Calculate the resonant frequency and angular frequency for an LC circuit with \( L = 3 \, \text{mH} \) and \( C = 3 \, \text{µF} \):

Input Values:
\( L = 3 \, \text{mH} = 3 \times 10^{-3} \, \text{H} \);
\( C = 3 \, \text{µF} = 3 \times 10^{-6} \, \text{F} \);
LC Product: \( L \times C = (3 \times 10^{-3}) \times (3 \times 10^{-6}) = 9 \times 10^{-9} \);
Resonant Frequency: \( f = \frac{1}{2 \pi \sqrt{L \times C}} = \frac{1}{2 \pi \sqrt{9 \times 10^{-9}}} \approx 1679.92 \, \text{Hz} \);
Angular Frequency: \( \omega = 2 \pi f = 2 \pi \times 1679.92 \approx 10555.8 \, \text{rad/s} = 10.5558 \, \text{krad/s} \);
Result: \( f = 1679.9200 \, \text{Hz} \), \( \omega = 10.5558 \, \text{krad/s} \).

5. Frequently Asked Questions (FAQ)

Q: What is the difference between resonant frequency and angular frequency?
A: Resonant frequency (\( f \)) is the frequency of oscillation in cycles per second (Hz), while angular frequency (\( \omega \)) is the rate of change of phase in radians per second (rad/s). They are related by \( \omega = 2 \pi f \).

Q: Why is the resonant frequency important in LC circuits?
A: The resonant frequency is the natural frequency at which the LC circuit oscillates with maximum amplitude, making it critical for applications like tuning radios, where the circuit must select a specific frequency from a complex signal.

Q: Can this calculator be used for RLC circuits?
A: No, this calculator assumes an ideal LC circuit with zero resistance. For RLC circuits, which include resistance, the resonant frequency calculation is the same, but the circuit’s behavior (e.g., damping) differs. You would need a different calculator for RLC circuits.