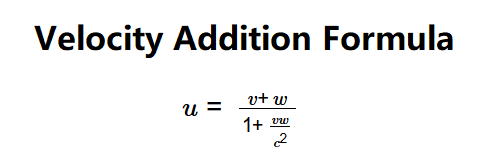Relativistic Velocity Addition Calculator

Spaceship Velocity (\( v \)):

Projectile Velocity (\( w \)):

1. What is Relativistic Velocity Addition Calculator?

Definition: This calculator computes the resultant velocity of a projectile as seen by an external observer when the projectile is launched from a moving spaceship, using the relativistic velocity addition formula.

Purpose: It is used to understand how velocities combine in special relativity, ensuring that the resultant velocity never exceeds the speed of light, unlike in classical physics where velocities simply add.

2. How Does the Calculator Work?

The calculator uses the following formula:

\( u = \frac{v + w}{1 + \frac{vw}{c^2}} \)

Where:

\( u \): Resultant velocity of the projectile as seen by an external observer
\( v \): Velocity of the spaceship
\( w \): Velocity of the projectile as seen from the spaceship
\( c \): Speed of light (\( 299,792,458 \, \text{m/s} \))

Steps:

Enter the spaceship velocity (\( v \)) with its respective unit (m/s, km/h, ft/s, mph, km/s, mi/s, c).
Enter the projectile velocity (\( w \)) with its respective unit (m/s, km/h, ft/s, mph, km/s, mi/s, c).
Convert both velocities to meters per second.
Calculate the resultant velocity using the relativistic velocity addition formula.
Convert the result to the selected output velocity unit.
Display the result with 4 decimal places.

3. Importance of Relativistic Velocity Addition

Calculating relativistic velocity addition is crucial for:

Space Travel: Understanding the combined velocities of objects in high-speed space missions.
Particle Physics: Analyzing the motion of particles moving at relativistic speeds.
Education: Demonstrating a key concept of Einstein’s special relativity, showing that velocities do not simply add as in classical physics.

4. Using the Calculator

Example: A spaceship travels at 0.6c, and it launches a projectile at 0.5c relative to the spaceship:

Spaceship Velocity (\( v \)): \( 0.6c = 0.6 \times 299,792,458 = 179,875,474.8 \) m/s
Projectile Velocity (\( w \)): \( 0.5c = 0.5 \times 299,792,458 = 149,896,229 \) m/s
Denominator: \( 1 + \frac{vw}{c^2} = 1 + \frac{(179,875,474.8 \times 149,896,229)}{(299,792,458)^2} = 1 + 0.3 = 1.3 \)
Resultant Velocity (\( u \)): \( \frac{179,875,474.8 + 149,896,229}{1.3} = \frac{329,771,703.8}{1.3} \approx 253,670,541.4 \) m/s
Convert to fraction of c: \( 253,670,541.4 / 299,792,458 \approx 0.8462 \)
Result: \( u = 0.8462 \) c

5. Frequently Asked Questions (FAQ)

Q: Why don’t velocities simply add in relativity?
A: In special relativity, the speed of light is the ultimate speed limit. The relativistic velocity addition formula ensures that the resultant velocity never exceeds \( c \), unlike in classical physics where velocities add directly.

Q: What happens at low speeds?
A: At low speeds (much less than \( c \)), the term \( \frac{vw}{c^2} \) becomes very small, and the formula approximates the classical addition: \( u \approx v + w \).

Q: Can the resultant velocity exceed the speed of light?
A: No, the formula ensures that \( u \) is always less than \( c \), even if \( v \) and \( w \) are close to \( c \). The calculator will display an error if either input velocity exceeds \( c \).