Reflection Coefficient Calculator

1. What is the Reflection Coefficient Calculator?

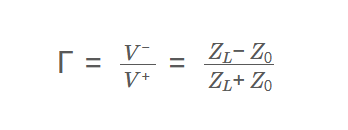
Definition: This calculator computes the reflection coefficient (\( \Gamma \)) of an RF transmission line, which indicates how much of an electromagnetic wave is reflected due to an impedance mismatch.

Purpose: It assists RF engineers, technicians, and students in analyzing impedance matching in RF systems, helping to optimize power transfer and minimize signal reflections.

2. How Does the Calculator Work?

The calculator uses the formula:

\( \Gamma = \frac{V^-}{V^+} = \frac{Z_L - Z_0}{Z_L + Z_0} \)

Where:

\( \Gamma \): Reflection coefficient (unitless)
\( V^- \): Reflected voltage wave
\( V^+ \): Incident voltage wave
\( Z_L \): Load impedance (ohms)
\( Z_0 \): Characteristic impedance (ohms)

Steps:

Enter the characteristic impedance (\( Z_0 \)) and load impedance (\( Z_L \)) in ohms.
Compute the reflection coefficient using the formula.
Take the magnitude of the result (since \( \Gamma \)) is complex, but we display the absolute value).
Display the result, formatted in scientific notation if the value is less than 0.001 or greater than 10000, otherwise with 4 decimal places.

3. Importance of Reflection Coefficient Calculation

Calculating the reflection coefficient is essential for:

Impedance Matching: Ensuring maximum power transfer by minimizing reflections in RF systems.
Signal Integrity: Reducing signal loss and interference in communication systems.
System Design: Evaluating RF components like antennas, amplifiers, and transmission lines.
Efficiency: Improving the performance of RF circuits by identifying mismatches.

4. Using the Calculator

Example 1: Calculate the reflection coefficient for a matched load:

Characteristic Impedance: \( Z_0 = 50 \, \text{ohms} \)
Load Impedance: \( Z_L = 50 \, \text{ohms} \)
Calculation:
- \( \Gamma = \frac{50 - 50}{50 + 50} = 0 \)
- Magnitude: \( |\Gamma| = 0 \)
Result: Reflection Coefficient (Γ) = 0.0000

Example 2: Calculate the reflection coefficient for an unmatched load:

Characteristic Impedance: \( Z_0 = 50 \, \text{ohms} \)
Load Impedance: \( Z_L = 75 \, \text{ohms} \)
Calculation:
- \( \Gamma = \frac{75 - 50}{75 + 50} = \frac{25}{125} = 0.2 \)
- Magnitude: \( |\Gamma| = 0.2 \)
Result: Reflection Coefficient (Γ) = 0.2000

5. Frequently Asked Questions (FAQ)

Q: Why is the reflection coefficient zero when impedances are matched?
A: When \( Z_L = Z_0 \), there is no impedance mismatch, so no power is reflected, resulting in \( \Gamma = 0 \).

Q: Why do I get an error for zero impedances?
A: The denominator (\( Z_L + Z_0 \)) must not be zero to avoid division by zero in the formula.

Q: What does a reflection coefficient of 1 mean?
A: A \( |\Gamma| = 1 \) indicates total reflection, which occurs with an open or short circuit (e.g., \( Z_L = 0 \) or \( Z_L \to \infty \)).

Q: Why is the result formatted in scientific notation?
A: Values less than 0.001 or greater than 10000 are displayed in scientific notation for readability.