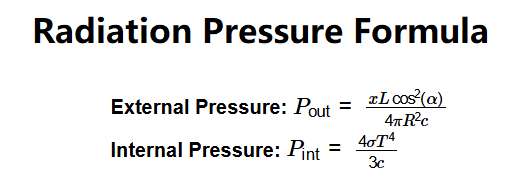1. What is Radiation Pressure Calculator?

Definition: This calculator computes the radiation pressure exerted by a star, either outside the star (\( P_{\text{out}} \)) or inside the star (\( P_{\text{int}} \)), based on the star's properties and the observer's position.

Purpose: It is used in astrophysics to understand the forces exerted by stellar radiation, which can affect phenomena like stellar winds, dust dynamics, and the internal structure of stars.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas:

• External Pressure: \( P_{\text{out}} = \frac{x L \cos^2(\alpha)}{4 \pi R^2 c} \)
• Internal Pressure: \( P_{\text{int}} = \frac{4 \sigma T^4}{3 c} \)

Where:

• \( P_{\text{out}} \): External radiation pressure (μPa, mPa, Pa, bar, psi, Torr)
• \( P_{\text{int}} \): Internal radiation pressure (μPa, mPa, Pa, bar, psi, Torr)
• \( x \): Surface type (\( x = 1 \) for opaque, \( x = 2 \) for reflective)
• \( L \): Luminosity of the star (W, GW, TW, PW, solar luminosities)
• \( \alpha \): Angle between the light beam and the surface (deg, rad)
• \( R \): Distance from the star (m, km, mi, ly, au, pc)
• \( c \): Speed of light (\( 299,792,458 \, \text{m/s} \))
• \( T \): Temperature of the star (K, °C, °F)
• \( \sigma \): Stefan-Boltzmann constant (\( 5.670367 \times 10^{-8} \, \text{W}/(\text{m}^2 \cdot \text{K}^4) \))

Unit Conversions:

• Luminosity (\( L \)):
  • 1 W = 1 W
  • 1 GW = \( 10^9 \) W
  • 1 TW = \( 10^{12} \) W
  • 1 PW = \( 10^{15} \) W
  • 1 solar luminosity = \( 3.828 \times 10^{26} \) W
• Distance (\( R \)):
  • 1 m = 1 m
  • 1 km = 1000 m
  • 1 mi = 1609.344 m
  • 1 ly = 9.4607304725808e15 m
  • 1 au = 1.496e11 m
  • 1 pc = 3.08568e16 m
• Angle (\( \alpha \)):
  • 1 deg = \( \frac{\pi}{180} \) rad
  • 1 rad = 1 rad
• Temperature (\( T \)):
  • 1 K = 1 K
  • 1 °C = K - 273.15
  • 1 °F = (K - 273.15) × 9/5 + 32
• Pressure (\( P \)):
  • 1 μPa = \( 10^{-6} \) Pa
  • 1 mPa = \( 10^{-3} \) Pa
  • 1 Pa = 1 Pa
  • 1 bar = 100,000 Pa
  • 1 psi = 6894.76 Pa
  • 1 Torr = 133.322 Pa

Steps:

• Select the calculation mode: external pressure (\( P_{\text{out}} \)) or internal pressure (\( P_{\text{int}} \)).
• For External Pressure:
  • Select the surface type (\( x \)): opaque (\( x = 1 \)) or reflective (\( x = 2 \)).
  • Enter the luminosity (\( L \)) with its respective unit (W, GW, TW, PW, solar luminosities).
  • Enter the distance (\( R \)) with its respective unit (m, km, mi, ly, au, pc).
  • Enter the angle (\( \alpha \)) with its respective unit (deg, rad).
  • Convert luminosity to watts, distance to meters, and angle to radians.
  • Calculate \( P_{\text{out}} = \frac{x L \cos^2(\alpha)}{4 \pi R^2 c} \).
• For Internal Pressure:
  • Enter the temperature (\( T \)) with its respective unit (K, °C, °F).
  • Convert temperature to Kelvin.
  • Calculate \( P_{\text{int}} = \frac{4 \sigma T^4}{3 c} \).
• Select the desired unit for the pressure result (μPa, mPa, Pa, bar, psi, Torr).
• Convert the pressure to the selected unit.
• Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Radiation Pressure Calculation

Calculating radiation pressure is crucial for:

• Stellar Dynamics: Radiation pressure affects stellar winds and the motion of dust particles around stars.
• Stellar Interiors: Internal radiation pressure plays a key role in the structure and stability of stars, especially massive ones.
• Space Technology: Understanding radiation pressure is essential for designing solar sails and other technologies that harness stellar radiation.

4. Using the Calculator

Examples:

• Example 1: Calculate the external radiation pressure from the Sun at 1 AU (\( L = 3.828 \times 10^{26} \, \text{W} \), \( R = 1 \, \text{AU} \), \( \alpha = 0^\circ \), \( x = 1 \)), with the result in microPascals:
  • Select External Pressure mode.
  • Select \( x = 1 \) (opaque surface).
  • Enter \( L = 3.828 \times 10^{26} \) W.
  • Enter \( R = 1 \) AU.
  • Convert to meters: \( R = 1 \times 1.496 \times 10^{11} = 1.496e11 \) m.
  • Enter \( \alpha = 0 \) degrees.
  • \( P_{\text{out}} = \frac{1 \times 3.828 \times 10^{26} \times \cos^2(0)}{4 \pi (1.496 \times 10^{11})^2 \times 299,792,458} \approx 4.54 \times 10^{-6} \) Pa
  • Convert to μPa: \( P_{\text{out}} = 4.54 \times 10^{-6} \times 10^6 = 4.54 \) μPa
  • Result: \( P_{\text{out}} = 4.5400 \) μPa
• Example 2: Calculate the internal radiation pressure inside the Sun (\( T = 5778 \, \text{K} \)), with the result in Torr:
  • Select Internal Pressure mode.
  • Enter \( T = 5778 \) K.
  • \( P_{\text{int}} = \frac{4 \times 5.670367 \times 10^{-8} \times (5778)^4}{3 \times 299,792,458} \approx 2.81 \times 10^5 \) Pa
  • Convert to Torr: \( P_{\text{int}} = 2.81 \times 10^5 \times 0.00750062 \approx 2107.67 \) Torr
  • Result: \( P_{\text{int}} = 2107.6700 \) Torr

5. Frequently Asked Questions (FAQ)

Q: What is radiation pressure?
A: Radiation pressure is the force per unit area exerted by electromagnetic radiation, such as light from a star, on a surface. It can be external (outside the star) or internal (inside the star).

Q: Why does the angle matter for external pressure?
A: The angle (\( \alpha \)) affects how much of the star's light directly impacts the surface. When \( \alpha = 0^\circ \), the light is perpendicular, maximizing the pressure; as \( \alpha \) increases, the pressure decreases due to the cosine term.

Q: How does temperature affect internal radiation pressure?
A: Internal radiation pressure depends on the fourth power of temperature (\( T^4 \)), so even small increases in temperature can significantly increase the pressure inside a star.

Radiation Pressure Calculator© - All Rights Reserved 2025