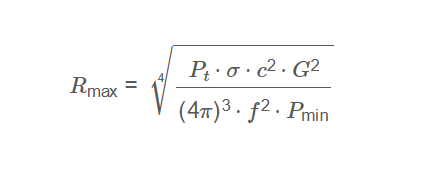Radar Maximum Range Calculator

Transmitted Power (\( P_t \)):

Antenna Gain (\( G \)):

Radar Cross Section (\( \sigma \)):

Radar Frequency (\( f \)):

Minimum Detectable Power (\( P_{\text{min}} \)):

1. What is a Radar Maximum Range Calculator?

Definition: This calculator determines the theoretical maximum range \( R_{\text{max}} \) of a radar system, which is the greatest distance at which a target can be detected, based on the transmitted power, antenna gain, radar cross section, radar frequency, and minimum detectable power.

Purpose: It helps radar engineers and system designers estimate the maximum detection range of a radar, aiding in system design and performance evaluation for applications like aviation, defense, weather monitoring, and marine navigation.

2. How Does the Calculator Work?

The calculator uses the following formula to compute the maximum range:

Maximum Range \( R_{\text{max}} \): \[ R_{\text{max}} = \sqrt[4]{\frac{P_t \cdot \sigma \cdot c^2 \cdot G^2}{(4\pi)^3 \cdot f^2 \cdot P_{\text{min}}}} \]

Where:

\( R_{\text{max}} \): Maximum range in meters
\( P_t \): Transmitted power in watts
\( \sigma \): Radar cross section in square meters (m²)
\( c \): Speed of light (\( 3 \times 10^8 \) m/s)
\( G \): Antenna gain (linear)
\( f \): Radar frequency in Hz
\( P_{\text{min}} \): Minimum detectable power in watts

Unit Conversions:

Input Power (\( P_t \), \( P_{\text{min}} \)):
1 mW = \( 10^{-3} \) W
1 dBm = \( 10^{\text{dBm}/10} \times 10^{-3} \) W
1 dBW = \( 10^{\text{dBW}/10} \) W
Input Gain (\( G \)):
\( G_{\text{linear}} = 10^{\frac{G_{\text{dB}}}{10}} \)
Input RCS (\( \sigma \)):
1 cm² = \( 10^{-4} \) m²
1 mm² = \( 10^{-6} \) m²
Input Frequency (\( f \)):
1 kHz = 1000 Hz
1 MHz = \( 10^6 \) Hz
1 GHz = \( 10^9 \) Hz
Output Range (\( R_{\text{max}} \)):
1 km = 1000 m
1 mile = 1609.34 m

Steps:

Enter the transmitted power \( P_t \), antenna gain \( G \), radar cross section \( \sigma \), radar frequency \( f \), and minimum detectable power \( P_{\text{min}} \), selecting the appropriate units for each.
Click "Calculate" to compute \( R_{\text{max}} \).
The result is initially displayed in meters (m).
Select a different unit for \( R_{\text{max}} \) (m, km, or miles) from the dropdown after the result to convert the displayed value.

3. Importance of Radar Maximum Range Calculation

Calculating the maximum range of a radar system is essential for:

Target Detection: Determines the farthest distance at which a radar can detect a target, critical for applications like aviation, defense, and weather monitoring.
System Design: Helps engineers optimize radar parameters like transmitted power, frequency, and gain to meet operational requirements.
Performance Evaluation: Provides a theoretical benchmark for radar performance, aiding in system validation and testing.

4. Using the Calculator

Examples:

Example 1: \( P_t = 1000 \) W, \( G = 1000 \) (linear), \( \sigma = 100 \) m², \( f = 10 \) GHz, \( P_{\text{min}} = 1 \times 10^{-12} \) W, Result in m
- Convert: \( f = 10 \times 10^9 = 10^{10} \, \text{Hz} \)
- Numerator: \( 1000 \times 100 \times (3 \times 10^8)^2 \times 1000^2 = 1000 \times 100 \times 9 \times 10^{16} \times 10^6 = 9 \times 10^{25} \)
- Denominator: \( (4\pi)^3 \times (10^{10})^2 \times 10^{-12} \approx 1984.4 \times 10^{20} \times 10^{-12} = 1.9844 \times 10^9 \)
- \( \frac{\text{Numerator}}{\text{Denominator}} = \frac{9 \times 10^{25}}{1.9844 \times 10^9} \approx 4.536 \times 10^{16} \)
- \( R_{\text{max}} = (4.536 \times 10^{16})^{1/4} \approx 82072.5 \, \text{m} \)
Example 2: \( P_t = 60 \) dBm, \( G = 30 \) dB, \( \sigma = 10000 \) cm², \( f = 10000 \) MHz, \( P_{\text{min}} = -90 \) dBm, Result in km
- Convert: \( P_t = 10^{60/10} \times 10^{-3} = 10^6 \times 10^{-3} = 1000 \, \text{W} \)
- \( G = 10^{30/10} = 1000 \)
- \( \sigma = 10000 \times 10^{-4} = 1 \, \text{m²} \)
- \( f = 10000 \times 10^6 = 10^{10} \, \text{Hz} \)
- \( P_{\text{min}} = 10^{-90/10} \times 10^{-3} = 10^{-9} \times 10^{-3} = 10^{-12} \, \text{W} \)
- Numerator: \( 1000 \times 1 \times (3 \times 10^8)^2 \times 1000^2 = 1000 \times 1 \times 9 \times 10^{16} \times 10^6 = 9 \times 10^{25} \)
- Same as Example 1: \( R_{\text{max}} \approx 82072.5 \, \text{m} \)
- Result in km: \( 82072.5 \div 1000 \approx 82.0725 \, \text{km} \)
Example 3: \( P_t = 30 \) dBW, \( G = 1000 \) (linear), \( \sigma = 100 \) m², \( f = 10 \) GHz, \( P_{\text{min}} = 1 \times 10^{-12} \) W, Result in miles
- Convert: \( P_t = 10^{30/10} = 1000 \, \text{W} \)
- Same as Example 1: \( R_{\text{max}} \approx 82072.5 \, \text{m} \)
- Result in miles: \( 82072.5 \div 1609.34 \approx 51.0058 \, \text{miles} \)

5. Frequently Asked Questions (FAQ)

Q: What limits the maximum range of a radar?
A: The maximum range is limited by factors like line of sight (due to antenna height and Earth's curvature), maximum unambiguous range (determined by PRF/PRT), and signal attenuation (due to atmospheric conditions or obstacles).

Q: Why does the formula use the fourth root?
A: The fourth root arises from the radar range equation, where the received power decreases with the fourth power of distance (\( 1/R^4 \)) due to the two-way path of the radar signal (transmit and receive).

Q: What factors affect the accuracy of this calculation?
A: The formula assumes ideal conditions (e.g., free space, no losses). Real-world factors like atmospheric attenuation, clutter, noise, and target characteristics can reduce the actual range, requiring further analysis or simulations.