RL Low-Pass Filter Calculator

1. What is RL Low-Pass Filter Calculator?

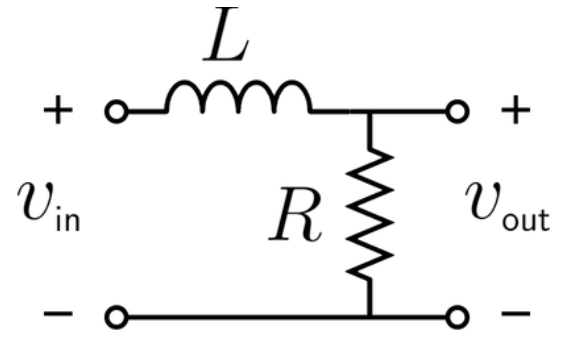
Definition: This calculator computes the cutoff frequency (\( f_c \)) for an RL low-pass filter, a basic electronic circuit that allows low-frequency signals to pass while attenuating high-frequency signals.

Purpose: It is used in electrical engineering to design RL low-pass filters for applications like signal processing, noise filtering, and RF circuits, where high-frequency signals need to be removed.

2. How Does the Calculator Work?

The calculator uses the following formula:

Cutoff Frequency: \( f_c = \frac{R}{2\pi L} \)

Where:

\( R \): Resistance (Ω)
\( L \): Inductance (H)
\( f_c \): Cutoff frequency (Hz)

Steps:

Enter the resistance (\( R \)) and inductance (\( L \)) with their units.
Convert all inputs to base units (Ω, H).
Calculate the cutoff frequency using the formula.
Convert the result to the selected output unit (Hz, kHz, MHz).
Display the result: if the value is less than 0.001 in the selected unit, use scientific notation; otherwise, display with 4 decimal places.

3. Importance of RL Low-Pass Filter Calculation

Calculating the cutoff frequency of an RL low-pass filter is crucial for:

Signal Processing: Ensuring that only low-frequency signals pass through, which is essential for applications like audio crossovers or noise filtering.
Circuit Design: Determining the cutoff frequency to design filters that meet specific frequency response requirements.
Frequency Separation: Using the inductor's frequency-dependent impedance to separate low-frequency signals from high-frequency ones in communication systems.

4. Using the Calculator

Example 1: Calculate the cutoff frequency for an RL low-pass filter with \( R = 100 \, \text{Ω} \) and \( L = 10 \, \text{mH} \):

Resistance (\( R \)): 100 Ω
Inductance (\( L \)): 10 mH = \( 0.01 \, \text{H} \)
Cutoff Frequency (\( f_c \)): \( \frac{100}{2\pi \cdot 0.01} \approx \frac{100}{0.06283} \approx 1591.55 \, \text{Hz} \), in kHz: \( 1.5916 \, \text{kHz} \)
Result: \( f_c = 1.5916 \, \text{kHz} \)

Example 2 (Demonstrating Scientific Notation): Calculate the cutoff frequency for an RL low-pass filter with \( R = 1 \, \text{kΩ} \) and \( L = 1 \, \text{µH} \):

Resistance (\( R \)): 1 kΩ = 1000 Ω
Inductance (\( L \)): 1 µH = \( 1 \times 10^{-6} \) H
Cutoff Frequency (\( f_c \)): \( \frac{1000}{2\pi \cdot 1 \times 10^{-6}} \approx \frac{1000}{6.283 \times 10^{-6}} \approx 159155000 \, \text{Hz} \), in MHz: \( 159155000 / 10^6 \approx 159.155 \, \text{MHz} \)
Result: \( f_c = 159.1550 \, \text{MHz} \)

5. Frequently Asked Questions (FAQ)

Q: What is an RL low-pass filter?
A: An RL low-pass filter is a simple electronic circuit consisting of a resistor (\( R \)) and an inductor (\( L \)) that allows low-frequency signals to pass while attenuating high-frequency signals above a certain cutoff frequency.

Q: Why is the cutoff frequency important?
A: The cutoff frequency (\( f_c \)) determines the point at which the filter starts to attenuate high-frequency signals. It is critical for ensuring the filter performs as intended in applications where high-frequency noise needs to be removed.

Q: How does the inductor’s impedance affect the filter’s performance?
A: The inductor’s impedance (\( Z_L \)) increases with frequency, making it act like an open circuit for high-frequency signals and a short circuit for low-frequency signals. This allows low-frequency signals to pass through to the output while high-frequency signals are attenuated.