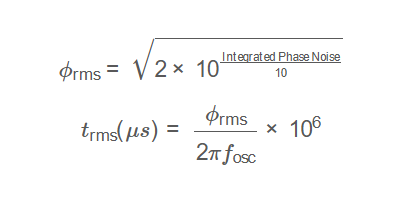RF Phase Noise to Phase Jitter Calculator

1. What is RF Phase Noise to Phase Jitter Calculator?

Definition: This calculator converts Integrated Phase Noise (in dBc) to RMS Phase Jitter in radians and microseconds, based on the oscillator frequency.

Purpose: It is used in RF engineering and telecommunications to quantify the timing jitter introduced by phase noise in oscillators and frequency sources.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas: \[ \phi_{\text{rms}} = \sqrt{2 \times 10^{\frac{\text{Integrated Phase Noise}}{10}}} \] \[ t_{\text{rms}} (\mu s) = \frac{\phi_{\text{rms}}}{2 \pi f_{\text{osc}}} \times 10^6 \] Where:

\( \phi_{\text{rms}} \): RMS Phase Jitter (radians)
\( t_{\text{rms}} \): RMS Phase Jitter (microseconds)
\( \text{Integrated Phase Noise} \): Total phase noise in dBc
\( f_{\text{osc}} \): Oscillator Frequency (Hz, kHz, MHz, GHz, THz)

Unit Conversions:

Oscillator Frequency (\( f_{\text{osc}} \)):
- 1 Hz = 1 Hertz
- 1 kHz = 1,000 Hz
- 1 MHz = 1,000,000 Hz
- 1 GHz = 1,000,000,000 Hz
- 1 THz = 1,000,000,000,000 Hz
Integrated Phase Noise: Measured in dBc, no conversion needed
RMS Phase Jitter (\( \phi_{\text{rms}} \)): Measured in radians, no conversion needed
RMS Phase Jitter (\( t_{\text{rms}} \)): Measured in microseconds (\( \mu s \)), converted from seconds by multiplying by \( 10^6 \)

Steps:

Enter the Oscillator Frequency and select the unit (Hz, kHz, MHz, GHz, THz).
Enter the Integrated Phase Noise in dBc.
Convert the Oscillator Frequency to Hertz.
Calculate \( \phi_{\text{rms}} = \sqrt{2 \times 10^{\frac{\text{Integrated Phase Noise}}{10}}} \).
Calculate \( t_{\text{rms}} (\mu s) = \frac{\phi_{\text{rms}}}{2 \pi f_{\text{osc}}} \times 10^6 \).
Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of RF Phase Noise to Phase Jitter Calculation

Calculating RMS Phase Jitter from Phase Noise is crucial for:

RF Engineering: Evaluating the timing accuracy of oscillators in RF systems.
Telecommunications: Ensuring signal integrity in high-speed communication systems by minimizing jitter.
Electronics: Designing stable clocks for digital systems, such as in data converters and PLLs.

4. Using the Calculator

Examples:

Example 1: For \( f_{\text{osc}} = 1 \, \text{GHz} \), Integrated Phase Noise = -40 dBc:
- Convert to Hertz: \( f_{\text{osc}} = 1,000,000,000 \, \text{Hz} \)
- \( \phi_{\text{rms}} = \sqrt{2 \times 10^{\frac{-40}{10}}} \)
- \( 10^{\frac{-40}{10}} = 10^{-4} = 0.0001 \)
- \( \phi_{\text{rms}} = \sqrt{2 \times 0.0001} = \sqrt{0.0002} \approx 0.0141 \, \text{radians} \)
- \( t_{\text{rms}} (\text{seconds}) = \frac{0.0141}{2 \pi \times 1,000,000,000} \approx 2.2498 \times 10^{-12} \, \text{seconds} \)
- \( t_{\text{rms}} (\mu s) = 2.2498 \times 10^{-12} \times 10^6 \approx 2.2498 \times 10^{-6} \, \mu s \)
Example 2: For \( f_{\text{osc}} = 100 \, \text{MHz} \), Integrated Phase Noise = -30 dBc:
- Convert to Hertz: \( f_{\text{osc}} = 100,000,000 \, \text{Hz} \)
- \( \phi_{\text{rms}} = \sqrt{2 \times 10^{\frac{-30}{10}}} \)
- \( 10^{\frac{-30}{10}} = 10^{-3} = 0.001 \)
- \( \phi_{\text{rms}} = \sqrt{2 \times 0.001} = \sqrt{0.002} \approx 0.0447 \, \text{radians} \)
- \( t_{\text{rms}} (\text{seconds}) = \frac{0.0447}{2 \pi \times 100,000,000} \approx 7.1138 \times 10^{-11} \, \text{seconds} \)
- \( t_{\text{rms}} (\mu s) = 7.1138 \times 10^{-11} \times 10^6 \approx 0.0711 \, \mu s \)

5. Frequently Asked Questions (FAQ)

Q: What is Integrated Phase Noise?
A: Integrated Phase Noise is the total phase noise power over a frequency range, expressed in dBc.

Q: What is RMS Phase Jitter?
A: RMS Phase Jitter is the root mean square phase deviation caused by phase noise, expressed in radians or microseconds.

Q: How is this conversion used in real life?
A: It is used in RF and communication systems to assess timing errors in oscillators, impacting signal quality in applications like radar and high-speed data transmission.