1. What is RC Time Constant Calculator?

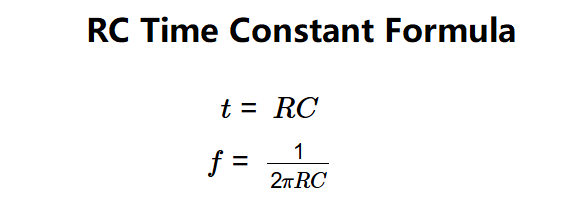
Definition: This calculator computes the time constant (\( t \)) and characteristic frequency (\( f \)) of an RC (resistor-capacitor) circuit.

Purpose: It is used in electronics to determine how quickly a capacitor charges or discharges in an RC circuit, and the frequency at which the circuit operates, which is essential for designing filters, timing circuits, and signal processing systems.

2. How Does the Calculator Work?

The calculator uses the following formulas for an RC circuit:

• \( t = RC \)
• \( f = \frac{1}{2 \pi RC} \)

Where:

• \( t \): Time constant (seconds);
• \( f \): Characteristic frequency (Hertz);
• \( R \): Resistance (Ohms);
• \( C \): Capacitance (Farads).

Steps:

• Enter the resistance (\( R \)) and capacitance (\( C \)) values with their units.
• Convert resistance to ohms and capacitance to farads.
• Calculate the time constant using \( t = RC \).
• Calculate the frequency using \( f = \frac{1}{2 \pi RC} \).
• Convert the time constant and frequency to the selected output units.
• Display the results with 4 decimal places.

3. Importance of RC Time Constant Calculation

Calculating the RC time constant and frequency is crucial for:

• Circuit Design: Designing low-pass or high-pass filters where the cutoff frequency depends on \( RC \).
• Timing Applications: Creating delays in circuits, such as in oscillators or timers.
• Signal Processing: Understanding how an RC circuit affects signal rise and fall times in amplifiers or integrators.

4. Using the Calculator

Example 1: Calculate the time constant and frequency of an RC circuit with \( R = 10 \, \text{kΩ} \) and \( C = 100 \, \text{µF} \):

• Input Values:
• \( R = 10 \, \text{kΩ} = 10 \times 10^3 = 10000 \, \text{Ω} \);
• \( C = 100 \, \text{µF} = 100 \times 10^{-6} = 0.0001 \, \text{F} \);
• Time constant: \( t = RC = 10000 \times 0.0001 = 1 \, \text{s} \);
• Frequency: \( f = \frac{1}{2 \pi RC} = \frac{1}{2 \pi \times 10000 \times 0.0001} \approx \frac{1}{2 \pi \times 1} \approx 0.1592 \, \text{Hz} \);
• Result: \( t = 1.0000 \, \text{s} \), \( f = 0.1592 \, \text{Hz} \).

Example 2: Calculate the time constant and frequency of an RC circuit with \( R = 1 \, \text{MΩ} \) and \( C = 1 \, \text{nF} \):

• Input Values:
• \( R = 1 \, \text{MΩ} = 1 \times 10^6 = 1000000 \, \text{Ω} \);
• \( C = 1 \, \text{nF} = 1 \times 10^{-9} = 0.000000001 \, \text{F} \);
• Time constant: \( t = RC = 1000000 \times 0.000000001 = 0.001 \, \text{s} = 1 \, \text{ms} \);
• Frequency: \( f = \frac{1}{2 \pi RC} = \frac{1}{2 \pi \times 1000000 \times 0.000000001} \approx \frac{1}{2 \pi \times 0.001} \approx 159.155 \, \text{Hz} \);
• Result: \( t = 1.0000 \, \text{ms} \), \( f = 0.1592 \, \text{kHz} \).

5. Frequently Asked Questions (FAQ)

Q: What does the RC time constant represent?
A: The RC time constant (\( t = RC \)) represents the time it takes for the capacitor to charge to approximately 63.2% of its final voltage (or discharge to 36.8% of its initial voltage) in an RC circuit.

Q: How does the time constant affect circuit behavior?
A: A larger time constant means the capacitor charges/discharges more slowly, leading to longer delays. A smaller time constant results in faster charging/discharging, useful for high-frequency applications.

Q: What is the significance of the characteristic frequency?
A: The characteristic frequency (\( f = \frac{1}{2 \pi RC} \)) is the cutoff frequency of the RC circuit, where the output amplitude drops to \( \frac{1}{\sqrt{2}} \) of the input amplitude in a filter application.

RC Time Constant Calculator© - All Rights Reserved 2025