Quartz Crystal Parameter Calculator

Series Inductance \( L_s \): ⓘ

Series Capacitance \( C_s \): ⓘ

Series Resistance \( R_s \) (Ω): ⓘ

Parallel Capacitance \( C_p \): ⓘ

Series Resonant Frequency (\( F_s \)):

Parallel Resonant Frequency (\( F_p \)):

Quality Factor (\( Q \)):

1. What are Quartz Crystal Parameters?

Definition: Quartz crystal parameters describe the electrical behavior of a quartz crystal in an oscillator circuit, including its series and parallel resonant frequencies and quality factor.

Purpose: These parameters are critical for designing stable oscillators in RF applications, such as frequency references in communication systems, clocks, and filters.

2. How Does the Calculator Work?

The calculator uses the following formulas for quartz crystal parameters:

Formula

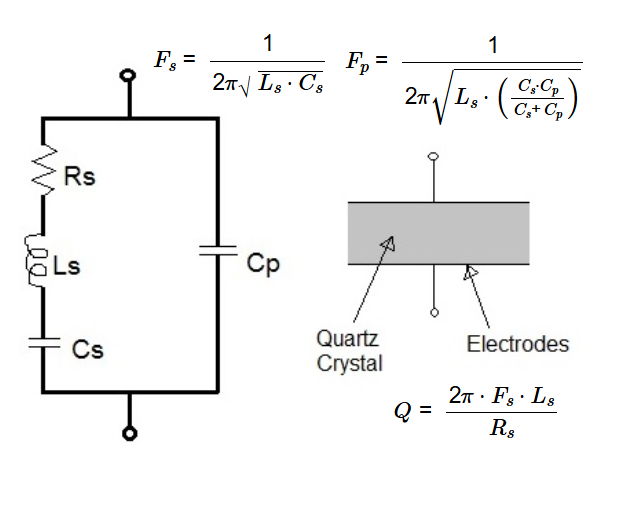
Series Resonance Frequency (\( F_s \)):
\[ F_s = \frac{1}{2\pi \sqrt{L_s \cdot C_s}} \]

Parallel Resonance Frequency (\( F_p \)):
\[ F_p = \frac{1}{2\pi \sqrt{L_s \cdot \left( \frac{C_s \cdot C_p}{C_s + C_p} \right)}} \]

Quality Factor (\( Q \)):
\[ Q = \frac{2\pi \cdot F_s \cdot L_s}{R_s} \]

Where, \( \pi = 3.14 \)

\( L_s \): Series Inductance (converted to henries from H, mH, or µH)
\( R_s \): Series Resistance (in ohms, \( \Omega \))
\( C_s \): Series Capacitance (converted to farads from F, nF, or pF)
\( C_p \): Parallel Capacitance (converted to farads from F, nF, or pF)

Steps:

Enter the series inductance \( L_s \), series capacitance \( C_s \), series resistance \( R_s \), and parallel capacitance \( C_p \), selecting their units.
Click "Calculate" to compute the series resonant frequency, parallel resonant frequency, and quality factor.
Select the output unit for frequencies (\( F_s \), \( F_p \)) (Hz, kHz, MHz) in the result section.
Results are displayed in the selected units (\( Q \) is unitless).

3. Importance of Quartz Crystal Parameters

Quartz crystal parameters are crucial for:

Frequency Stability: Ensures precise frequency control in oscillators for communication systems.
Filter Design: Determines the bandwidth and selectivity of crystal filters in RF circuits.
Performance Optimization: High \( Q \) values indicate low energy loss, improving oscillator efficiency.

4. Using the Calculator

Examples:

Example 1: Typical Quartz Crystal (Frequencies in MHz)
- \( L_s = 10 \, \text{mH}, C_s = 2 \, \text{pF}, R_s = 50 \, \Omega, C_p = 5 \, \text{pF} \)
- Convert: \( L_s = 0.01 \, \text{H}, C_s = 2 \times 10^{-12} \, \text{F}, C_p = 5 \times 10^{-12} \, \text{F} \)
- \( F_s = \frac{1}{2 \pi \sqrt{0.01 \times 2 \times 10^{-12}}} \approx 3,559,654 \, \text{Hz} \approx 3.56 \, \text{MHz} \)
- \( F_p = \frac{1}{2 \pi \sqrt{0.01 \times 1.4286 \times 10^{-12}}} \approx 4,207,228 \, \text{Hz} \approx 4.21 \, \text{MHz} \)
- \( Q = \frac{2 \pi \times 3,559,654 \times 0.01}{50} \approx 4,472.35 \)
Example 2: Small Inductance (Frequencies in kHz)
- \( L_s = 100 \, \text{µH}, C_s = 10 \, \text{pF}, R_s = 20 \, \Omega, C_p = 2 \, \text{pF} \)
- Convert: \( L_s = 0.0001 \, \text{H}, C_s = 10 \times 10^{-12} \, \text{F}, C_p = 2 \times 10^{-12} \, \text{F} \)
- \( F_s \approx 5,032,921 \, \text{Hz} \approx 5,032.92 \, \text{kHz} \)
- \( F_p \approx 6,164,315 \, \text{Hz} \approx 6,164.32 \, \text{kHz} \)
- \( Q \approx 1,581.14 \)
Example 3: High Resistance (Frequencies in Hz)
- \( L_s = 1 \, \text{H}, C_s = 1 \, \text{nF}, R_s = 1000 \, \Omega, C_p = 100 \, \text{pF} \)
- Convert: \( C_s = 1 \times 10^{-9} \, \text{F}, C_p = 100 \times 10^{-12} \, \text{F} \)
- \( F_s \approx 5,032.92 \, \text{Hz} \)
- \( F_p \approx 16,726.94 \, \text{Hz} \)
- \( Q \approx 3.16 \)

5. Frequently Asked Questions (FAQ)

Q: What is the difference between series and parallel resonant frequencies?
A: The series resonant frequency (\( F_s \)) is the frequency at which the crystal's impedance is purely resistive (minimum). The parallel resonant frequency (\( F_p \)) is higher, where the crystal's impedance peaks due to the parallel capacitance \( C_p \).

Q: Why is the quality factor \( Q \) important?
A: A high \( Q \) indicates low energy loss in the crystal, leading to sharper resonance and better frequency stability in oscillator circuits.

Q: How does unit conversion work in the calculator?
A: The calculator converts inductance to henries (e.g., 1000 mH = 1 H), capacitance to farads (e.g., 1 pF = \( 10^{-12} \) F), and frequencies to the selected unit (e.g., 1,000,000 Hz = 1 MHz).