Projectile Range Calculator

Projectile Range Calculator With Angle

Input Method:

Initial Velocity (V₀):

Launch Angle (α):

Horizontal Velocity (V_x):

Vertical Velocity (V_y):

Initial Height (h):

Gravitational Acceleration (g):

Horizontal and Vertical Velocities

Horizontal Velocity (V_x):

Vertical Velocity (V_y):

Range (R):

1. What is a Projectile Range Calculator?

Definition: This calculator determines the horizontal range of a projectile, along with its horizontal and vertical velocity components, given the initial conditions.

Purpose: It is used in physics to analyze the horizontal distance traveled by a projectile, aiding in understanding projectile motion in ballistics, sports, and engineering.

2. How Does the Calculator Work?

The calculator supports two input methods:

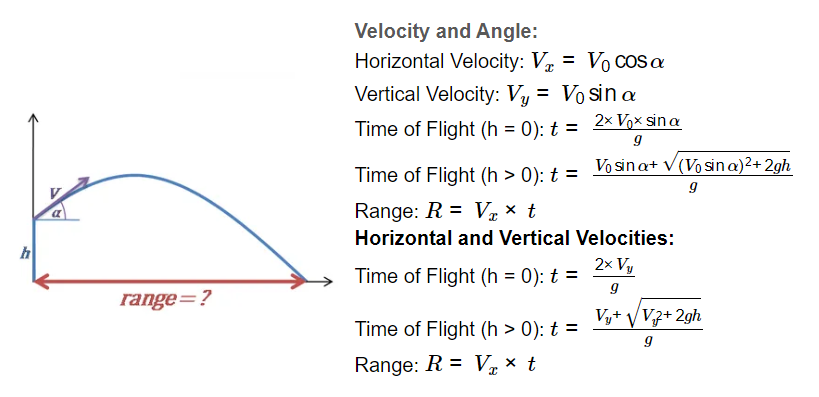
Velocity and Angle:

Horizontal Velocity: \( V_x = V_0 \cos \alpha \)
Vertical Velocity: \( V_y = V_0 \sin \alpha \)
Time of Flight (h = 0): \( t = \frac{2 \times V_0 \times \sin \alpha}{g} \)
Time of Flight (h > 0): \( t = \frac{V_0 \sin \alpha + \sqrt{(V_0 \sin \alpha)^2 + 2gh}}{g} \)
Range: \( R = V_x \times t \)

Horizontal and Vertical Velocities:

Time of Flight (h = 0): \( t = \frac{2 \times V_y}{g} \)
Time of Flight (h > 0): \( t = \frac{V_y + \sqrt{V_y^2 + 2gh}}{g} \)
Range: \( R = V_x \times t \)

Where:

\( R \): Range (cm, m, in, ft, yd, km, mi)
\( V_x \): Horizontal velocity (m/s, km/h, ft/s, mph, kn, ft/min)
\( V_y \): Vertical velocity (m/s, km/h, ft/s, mph, kn, ft/min)
\( V_0 \): Initial velocity (m/s, km/h, ft/s, mph, kn, ft/min)
\( \alpha \): Launch angle (degrees, radians)
\( h \): Initial height (cm, m, in, ft, yd, km, mi)
\( g \): Gravitational acceleration (m/s², ft/s²)

Unit Conversions:

Velocity Units (V₀, V_x, V_y): m/s, km/h, ft/s, mph, kn, ft/min
Angle Units (α): degrees, radians
Height Units (h, R): cm, m, in, ft, yd, km, mi
Gravity Units (g): m/s², ft/s²

Steps:

Select the input method (Velocity and Angle or Horizontal and Vertical Velocities)
Enter the required velocity and angle or velocity components, selecting the units
Enter the initial height (h), selecting the unit
Enter the gravitational acceleration (g), selecting the unit (default is 9.81 m/s²)
Convert all inputs to SI units (m/s, radians, m, m/s²)
Calculate the horizontal and vertical velocities (if using velocity and angle)
Calculate the time of flight and range
Select the desired units for the results and view the values

3. Importance of Projectile Range Calculation

Calculating the projectile range is crucial for:

Physics Education: Understanding the horizontal component of projectile motion.
Sports and Ballistics: Predicting the distance a ball or projectile will travel.
Engineering and Safety: Designing trajectories for safety in scenarios like artillery or sports equipment.

4. Using the Calculator

Examples:

Example 1 (Velocity and Angle, h = 12 m): Initial velocity \( V_0 = 25 \, \text{m/s} \), angle \( \alpha = 12^\circ \), initial height \( h = 12 \, \text{m} \), gravity \( g = 9.81 \, \text{m/s}^2 \):
- Angle in radians = \( 12 \times \frac{\pi}{180} = 0.2094 \, \text{rad} \)
- Horizontal velocity = \( 25 \cos(0.2094) = 24.451 \, \text{m/s} \)
- Vertical velocity = \( 25 \sin(0.2094) = 5.201 \, \text{m/s} \)
- Time of flight = \( \frac{5.201 + \sqrt{(5.201)^2 + 2 \times 9.81 \times 12}}{9.81} = \frac{5.201 + \sqrt{27.05 + 235.44}}{9.81} = \frac{5.201 + 16.197}{9.81} = 2.181 \, \text{s} \)
- Range = \( 24.451 \times 2.181 = 53.335 \, \text{m} \)
Example 2 (Horizontal and Vertical Velocities, h = 0): Horizontal velocity \( V_x = 20 \, \text{m/s} \), vertical velocity \( V_y = 10 \, \text{m/s} \), initial height \( h = 0 \, \text{m} \), gravity \( g = 9.81 \, \text{m/s}^2 \):
- Time of flight = \( \frac{2 \times 10}{9.81} = 2.038 \, \text{s} \)
- Range = \( 20 \times 2.038 = 40.760 \, \text{m} \)

5. Frequently Asked Questions (FAQ)

Q: What is the projectile range?
A: The projectile range (\( R \)) is the horizontal distance traveled by a projectile from launch to landing.

Q: Why does initial height affect the range?
A: A non-zero initial height increases the time of flight, allowing the projectile to travel a greater horizontal distance.

Q: What happens if the launch angle is 0°?
A: At 0°, the projectile travels horizontally, and the range depends on the initial height and velocity, but the vertical velocity is 0.