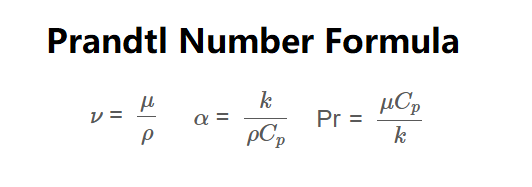1. What is Prandtl Number Calculator?
Definition: This calculator computes the momentum diffusivity (\( \nu \)), thermal diffusivity (\( \alpha \)), and Prandtl number (\( \text{Pr} \)) of a fluid, based on its density (\( \rho \)), dynamic viscosity (\( \mu \)), specific heat (\( C_p \)), and thermal conductivity (\( k \)).
Purpose: It is used in fluid dynamics and heat transfer to characterize the relative thickness of the momentum and thermal boundary layers, aiding in the design of heat exchangers, convection systems, and fluid flow processes.
2. How Does the Calculator Work?
The calculator uses the following formulas:
Formulas:
\[
\nu = \frac{\mu}{\rho}
\]
\[
\alpha = \frac{k}{\rho C_p}
\]
\[
\text{Pr} = \frac{\mu C_p}{k}
\]
Where:
- \( \nu \): Momentum diffusivity (m²/s, ft²/s)
- \( \mu \): Dynamic viscosity (Pa·s, psi·s)
- \( \rho \): Density (kg/m³, lb/ft³)
- \( \alpha \): Thermal diffusivity (m²/s, ft²/s)
- \( k \): Thermal conductivity (W/(m·K), BTU/(h·ft·°F))
- \( C_p \): Specific heat at constant pressure (J/(kg·K), BTU/(lb·°F))
- \( \text{Pr} \): Prandtl number (dimensionless)
Predefined Fluid Data:
- Air: \( \rho = 1.2047 \, \text{kg/m³} \), \( \mu = 2.6404 \times 10^{-9} \, \text{psi·s} \), \( C_p = 0.24035 \, \text{BTU/(lb·°F)} \), \( k = 0.0148 \, \text{BTU/(h·ft·°F)} \)
- Water: \( \rho = 997 \, \text{kg/m³} \), \( \mu = 1.4533 \times 10^{-7} \, \text{psi·s} \), \( C_p = 0.999 \, \text{BTU/(lb·°F)} \), \( k = 0.35095 \, \text{BTU/(h·ft·°F)} \)
- Sodium: \( \rho = 968 \, \text{kg/m³} \), \( \mu = 7.861 \times 10^{-8} \, \text{psi·s} \), \( C_p = 0.29267 \, \text{BTU/(lb·°F)} \), \( k = 34.69 \, \text{BTU/(h·ft·°F)} \)
- Methanol: \( \rho = 791.4 \, \text{kg/m³} \), \( \mu = 7.89 \times 10^{-8} \, \text{psi·s} \), \( C_p = 0.5999 \, \text{BTU/(lb·°F)} \), \( k = 0.11564 \, \text{BTU/(h·ft·°F)} \)
- Mercury: \( \rho = 13600 \, \text{kg/m³} \), \( \mu = 2.2133 \times 10^{-7} \, \text{psi·s} \), \( C_p = 0.033684 \, \text{BTU/(lb·°F)} \), \( k = 4.77 \, \text{BTU/(h·ft·°F)} \)
- Krypton: \( \rho = 3.74 \, \text{kg/m³} \), \( \mu = 0.000003713 \, \text{psi·s} \), \( C_p = 0.05925 \, \text{BTU/(lb·°F)} \), \( k = 0.005452 \, \text{BTU/(h·ft·°F)} \)
Unit Conversions:
- Density (\( \rho \)):
- 1 kg/m³ = 1 kg/m³
- 1 lb/ft³ = 16.0185 kg/m³
- Dynamic Viscosity (\( \mu \)):
- 1 Pa·s = 1 Pa·s
- 1 psi·s = 6894.76 Pa·s
- Specific Heat (\( C_p \)):
- 1 J/(kg·K) = 1 J/(kg·K)
- 1 BTU/(lb·°F) = 4186.8 J/(kg·K)
- Thermal Conductivity (\( k \)):
- 1 W/(m·K) = 1 W/(m·K)
- 1 BTU/(h·ft·°F) = 1.7307 W/(m·K)
- Momentum and Thermal Diffusivity (\( \nu \), \( \alpha \)):
- 1 m²/s = 1 m²/s
- 1 ft²/s = \( (0.3048)^2 \) m²/s
Steps:
- Select a fluid from the dropdown or choose "Custom" to enter your own values.
- If a predefined fluid is selected, the fields for density, viscosity, specific heat, and thermal conductivity will auto-fill with default units (kg/m³, psi·s, BTU/(lb·°F), BTU/(h·ft·°F)) and become read-only.
- Enter the density (\( \rho \)) with its respective unit (kg/m³, lb/ft³).
- Enter the dynamic viscosity (\( \mu \)) with its respective unit (psi·s, Pa·s).
- Enter the specific heat (\( C_p \)) with its respective unit (BTU/(lb·°F), J/(kg·K)).
- Enter the thermal conductivity (\( k \)) with its respective unit (BTU/(h·ft·°F), W/(m·K)).
- Convert all inputs to SI units (kg/m³ for \( \rho \), Pa·s for \( \mu \), J/(kg·K) for \( C_p \), W/(m·K) for \( k \)).
- Calculate the momentum diffusivity (\( \nu \)), thermal diffusivity (\( \alpha \)), and Prandtl number (\( \text{Pr} \)) using the formulas.
- Convert the diffusivities to the selected units and display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.
3. Importance of Prandtl Number Calculation
Calculating the Prandtl number and diffusivities is crucial for:
- Heat Transfer Analysis: Understanding the relative rates of momentum and heat transfer in fluid flow, essential for designing heat exchangers and cooling systems.
- Fluid Dynamics: Predicting flow behavior in engineering applications, such as aerodynamics and hydrodynamics.
- Material Selection: Choosing fluids with appropriate properties for specific thermal and flow conditions in industrial processes.
4. Using the Calculator
Examples:
- Example 1: Calculate the momentum diffusivity, thermal diffusivity, and Prandtl number for Water, with momentum and thermal diffusivity in m²/s:
- Select "Water" (auto-fills: \( \rho = 997 \, \text{kg/m³} \), \( \mu = 1.4533 \times 10^{-7} \, \text{psi·s} \), \( C_p = 0.999 \, \text{BTU/(lb·°F)} \), \( k = 0.35095 \, \text{BTU/(h·ft·°F)} \)).
- Convert \( \mu \): \( 1.4533 \times 10^{-7} \times 6894.76 = 0.001002 \, \text{Pa·s} \)
- Convert \( C_p \): \( 0.999 \times 4186.8 = 4182.6132 \, \text{J/(kg·K)} \)
- Convert \( k \): \( 0.35095 \times 1.7307 = 0.60729 \, \text{W/(m·K)} \)
- Momentum diffusivity: \( \nu = \frac{0.001002}{997} = 1.0050 \times 10^{-6} \, \text{m²/s} \)
- Thermal diffusivity: \( \alpha = \frac{0.60729}{997 \times 4182.6132} = 1.4573 \times 10^{-7} \, \text{m²/s} \)
- Prandtl number: \( \text{Pr} = \frac{0.001002 \times 4182.6132}{0.60729} = 6.8946 \)
- Result: \( \nu = 1.0050 \times 10^{-6} \, \text{m²/s} \), \( \alpha = 1.4573 \times 10^{-7} \, \text{m²/s} \), \( \text{Pr} = 6.8946 \)
- Example 2: Calculate the momentum diffusivity, thermal diffusivity, and Prandtl number for a custom fluid with density 1000 kg/m³, dynamic viscosity 0.002 Pa·s, specific heat 2000 J/(kg·K), and thermal conductivity 0.5 W/(m·K), with momentum and thermal diffusivity in ft²/s:
- Select "Custom".
- Enter \( \rho = 1000 \) kg/m³.
- Enter \( \mu = 0.002 \) Pa·s.
- Enter \( C_p = 2000 \) J/(kg·K).
- Enter \( k = 0.5 \) W/(m·K).
- Momentum diffusivity: \( \nu = \frac{0.002}{1000} = 2 \times 10^{-6} \, \text{m²/s} \)
- Convert to ft²/s: \( \nu = 2 \times 10^{-6} \div (0.3048)^2 = 2.1528 \times 10^{-5} \, \text{ft²/s} \)
- Thermal diffusivity: \( \alpha = \frac{0.5}{1000 \times 2000} = 2.5 \times 10^{-7} \, \text{m²/s} \)
- Convert to ft²/s: \( \alpha = 2.5 \times 10^{-7} \div (0.3048)^2 = 2.6910 \times 10^{-6} \, \text{ft²/s} \)
- Prandtl number: \( \text{Pr} = \frac{0.002 \times 2000}{0.5} = 8 \)
- Result: \( \nu = 2.1528 \times 10^{-5} \, \text{ft²/s} \), \( \alpha = 2.6910 \times 10^{-6} \, \text{ft²/s} \), \( \text{Pr} = 8.0000 \)
5. Frequently Asked Questions (FAQ)
Q: What does the Prandtl number represent?
A: The Prandtl number (\( \text{Pr} \)) is the ratio of momentum diffusivity to thermal diffusivity, indicating the relative thickness of the momentum and thermal boundary layers in fluid flow.
Q: What is the significance of momentum and thermal diffusivity?
A: Momentum diffusivity (\( \nu \)) describes the rate of momentum transfer, while thermal diffusivity (\( \alpha \)) describes the rate of heat transfer within a fluid, both critical for understanding flow and heat transfer behavior.
Q: Why are predefined fluid values provided?
A: Predefined fluid values simplify calculations by providing typical properties for common fluids, allowing users to quickly compute values without needing to look up data.
Prandtl Number Calculator© - All Rights Reserved 2025
 Home
Home
 Back
Back