Polar Moment of Inertia Calculator

Cross-Section Type:

Radius (R):

Inner Radius (R_i):

Outer Radius (R):

1. What is a Polar Moment of Inertia Calculator?

Definition: This calculator determines the polar moment of inertia (\( J \)) of a circular cross-section, either solid or hollow, which measures resistance to torsional deformation.

Purpose: It is used in engineering to analyze the torsional behavior of beams or shafts, aiding in the design of structures and mechanical components.

2. How Does the Calculator Work?

The calculator supports two types of circular cross-sections:

Solid Circular Section: \[ J = \frac{\pi R^4}{2} \] Hollow Circular Section: \[ J = \frac{\pi}{2} (R^4 - R_i^4) \] Where:

\( J \): Polar moment of inertia (mm⁴, cm⁴, in⁴, ft⁴)
\( R \): Outer radius (mm/cm/m/in/ft)
\( R_i \): Inner radius (mm/cm/m/in/ft for hollow)
\( D \): Outer diameter (calculated as \( 2 \times R \))
\( d \): Inner diameter (calculated as \( 2 \times R_i \))

All dimensions are converted to cm for calculation, and the result is in cm⁴ before being converted to the selected output unit.

Unit Conversions:

Dimension Units (R, R_i): mm, cm, m, in, ft
Polar Moment Units (J): mm⁴, cm⁴, in⁴, ft⁴

Steps:

Select the cross-section type (Solid or Hollow)
Enter the radius (R), selecting the unit
For hollow sections, enter the inner radius (R_i), selecting the unit
Convert all inputs to cm
Calculate the polar moment of inertia in cm⁴
Convert the result to the selected output unit
Calculate and display the diameter (D) for solid sections, and both diameters (D and d) for hollow sections
View the result

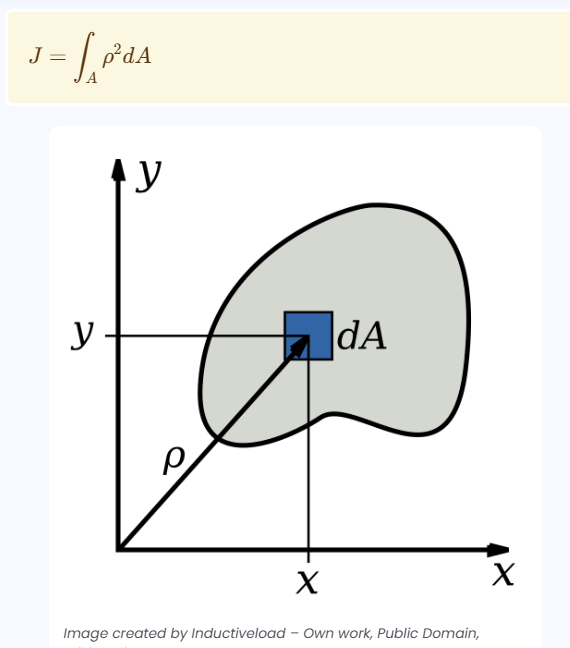
3. Importance of Polar Moment of Inertia Calculation

Calculating the polar moment of inertia is crucial for:

Engineering Design: Designing beams and shafts to withstand torsional loads.
Structural Analysis: Predicting how materials will deform under twisting forces.
Mechanical Systems: Ensuring the stability and safety of rotating components like axles and driveshafts.

4. Using the Calculator

Examples:

Example 1 (Solid Section): Radius \( R = 2.5 \, \text{cm} \):
- Radius in cm = \( 2.5 \, \text{cm} \)
- Polar moment = \( \frac{\pi (2.5)^4}{2} = \frac{\pi \times 39.0625}{2} = 61.364 \, \text{cm}^4 \)
- In mm⁴ = \( 61.364 \times 10000 = 613640.304 \, \text{mm}^4 \)
- Diameter = \( 2 \times 2.5 = 5.000 \, \text{cm} \)
Example 2 (Hollow Section): Outer radius \( R = 12 \, \text{cm} \), inner radius \( R_i = 2.5 \, \text{cm} \):
- Outer radius in cm = \( 12 \, \text{cm} \)
- Inner radius in cm = \( 2.5 \, \text{cm} \)
- Polar moment = \( \frac{\pi}{2} \left( (12)^4 - (2.5)^4 \right) = \frac{\pi}{2} \left( 20736 - 39.0625 \right) = \frac{\pi}{2} \times 20696.9375 = 32504.908 \, \text{cm}^4 \)
- In mm⁴ = \( 32504.908 \times 10000 = 325049080.484 \, \text{mm}^4 \)
- Outer diameter = \( 12 \times 2 = 24.000 \, \text{cm} \)
- Inner diameter = \( 2.5 \times 2 = 5.000 \, \text{cm} \)

5. Frequently Asked Questions (FAQ)

Q: What is the polar moment of inertia?
A: The polar moment of inertia (\( J \)) measures a cross-section's resistance to torsional deformation, calculated based on its geometry.

Q: Why is the polar moment different for solid and hollow sections?
A: Hollow sections have less material near the center, reducing their polar moment compared to a solid section of the same outer radius.

Q: How does the polar moment of inertia affect design?
A: A higher polar moment of inertia indicates greater resistance to twisting, which is critical for designing stable beams and shafts under torsional loads.