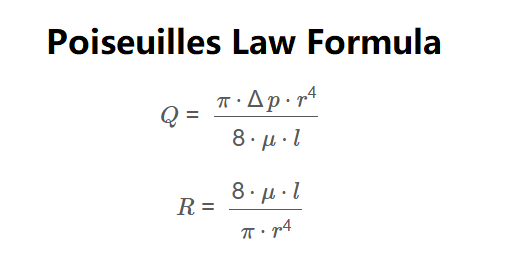Poiseuille's Law Calculator

Pressure Change (\( \Delta p \)):

Pipe Radius (\( r \)):

Dynamic Viscosity (\( \mu \)):

Pipe Length (\( l \)):

Flow Rate (\( Q \)):

Flow Resistance (\( R \)):

1. What is Poiseuille's Law Calculator?

Definition: This calculator computes the flow rate (\( Q \)) and flow resistance (\( R \)) of a fluid through a cylindrical pipe using Poiseuille's Law, based on the pressure change (\( \Delta p \)), pipe radius (\( r \)), dynamic viscosity (\( \mu \)), and pipe length (\( l \)).

Purpose: It is used in fluid dynamics to analyze laminar flow in pipes, applicable in fields like hydraulics, medical fluid dynamics (e.g., blood flow), and engineering design.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas: \[ Q = \frac{\pi \cdot \Delta p \cdot r^4}{8 \cdot \mu \cdot l} \] \[ R = \frac{8 \cdot \mu \cdot l}{\pi \cdot r^4} \] Where:

\( Q \): Flow rate (m³/s, L/s, m³/min, ft³/s, ft³/min)
\( \pi \): Pi constant, approximately 3.14159
\( \Delta p \): Pressure change (Pa, kPa, bar, psi)
\( r \): Pipe radius (m, cm, mm, in)
\( \mu \): Dynamic viscosity (Pa·s, P, cP)
\( l \): Pipe length (m, cm, mm, in)
\( R \): Flow resistance (Pa·s/m³, Pa·s/L)

Unit Conversions:

Pressure Change (\( \Delta p \)):
- 1 Pa = 1 Pa
- 1 kPa = 1000 Pa
- 1 bar = 100000 Pa
- 1 psi = 6894.76 Pa
Radius (\( r \)) and Length (\( l \)):
- 1 m = 1 m
- 1 cm = 0.01 m
- 1 mm = 0.001 m
- 1 in = 0.0254 m
Dynamic Viscosity (\( \mu \)):
- 1 Pa·s = 1 Pa·s
- 1 P = 0.1 Pa·s
- 1 cP = 0.001 Pa·s
Flow Rate (\( Q \)):
- 1 m³/s = 1 m³/s
- 1 L/s = 0.001 m³/s
- 1 m³/min = \( \frac{1}{60} \) m³/s
- 1 ft³/s = \( (0.3048)^3 \) m³/s
- 1 ft³/min = \( \frac{(0.3048)^3}{60} \) m³/s
Flow Resistance (\( R \)):
- 1 Pa·s/m³ = 1 Pa·s/m³
- 1 Pa·s/L = 1000 Pa·s/m³

Steps:

Enter the pressure change (\( \Delta p \)) with its respective unit (Pa, kPa, bar, psi).
Enter the pipe radius (\( r \)) with its respective unit (m, cm, mm, in).
Enter the dynamic viscosity (\( \mu \)) with its respective unit (Pa·s, P, cP).
Enter the pipe length (\( l \)) with its respective unit (m, cm, mm, in).
Convert all inputs to SI units (Pa for \( \Delta p \), m for \( r \) and \( l \), Pa·s for \( \mu \)).
Calculate the flow rate (\( Q \)) and flow resistance (\( R \)) using the formulas.
Convert the results to the selected units and display them, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Poiseuille's Law Calculation

Calculating flow rate and resistance using Poiseuille's Law is crucial for:

Hydraulic Systems: Designing efficient piping systems for fluid transport in engineering applications.
Medical Applications: Analyzing blood flow in vessels for medical diagnostics and treatments.
Industrial Processes: Optimizing fluid flow in manufacturing processes, such as in chemical reactors or cooling systems.

4. Using the Calculator

Examples:

Example 1: Calculate the flow rate and resistance for a pipe with a pressure change of 1000 Pa, radius of 2 mm, dynamic viscosity of 0.001 Pa·s, and length of 1 m, with flow rate in L/s and resistance in Pa·s/L:
- Enter \( \Delta p = 1000 \) Pa.
- Enter \( r = 2 \) mm.
- Convert to m: \( r = 2 \times 0.001 = 0.002 \, \text{m} \)
- Enter \( \mu = 0.001 \) Pa·s.
- Enter \( l = 1 \) m.
- Flow rate: \( Q = \frac{\pi \times 1000 \times (0.002)^4}{8 \times 0.001 \times 1} = 6.2832 \times 10^{-6} \, \text{m³/s} \)
- Convert to L/s: \( Q = 6.2832 \times 10^{-6} \times 1000 = 0.0063 \, \text{L/s} \)
- Flow resistance: \( R = \frac{8 \times 0.001 \times 1}{\pi \times (0.002)^4} = 1.5915 \times 10^8 \, \text{Pa·s/m³} \)
- Convert to Pa·s/L: \( R = 1.5915 \times 10^8 \times 0.001 = 1.5915 \times 10^5 \, \text{Pa·s/L} \)
- Result: \( Q = 0.0063 \, \text{L/s} \), \( R = 1.5915 \times 10^5 \, \text{Pa·s/L} \)
Example 2: Calculate the flow rate and resistance for a pipe with a pressure change of 0.5 bar, radius of 0.1 in, dynamic viscosity of 1 cP, and length of 50 cm, with flow rate in ft³/min and resistance in Pa·s/m³:
- Enter \( \Delta p = 0.5 \) bar.
- Convert to Pa: \( \Delta p = 0.5 \times 100000 = 50000 \, \text{Pa} \)
- Enter \( r = 0.1 \) in.
- Convert to m: \( r = 0.1 \times 0.0254 = 0.00254 \, \text{m} \)
- Enter \( \mu = 1 \) cP.
- Convert to Pa·s: \( \mu = 1 \times 0.001 = 0.001 \, \text{Pa·s} \)
- Enter \( l = 50 \) cm.
- Convert to m: \( l = 50 \times 0.01 = 0.5 \, \text{m} \)
- Flow rate: \( Q = \frac{\pi \times 50000 \times (0.00254)^4}{8 \times 0.001 \times 0.5} = 1.6275 \times 10^{-5} \, \text{m³/s} \)
- Convert to ft³/min: \( Q = 1.6275 \times 10^{-5} \times \frac{60}{(0.3048)^3} = 0.0345 \, \text{ft³/min} \)
- Flow resistance: \( R = \frac{8 \times 0.001 \times 0.5}{\pi \times (0.00254)^4} = 3.0714 \times 10^7 \, \text{Pa·s/m³} \)
- Result: \( Q = 0.0345 \, \text{ft³/min} \), \( R = 3.0714 \times 10^7 \, \text{Pa·s/m³} \)

5. Frequently Asked Questions (FAQ)

Q: What does Poiseuille's Law describe?
A: Poiseuille's Law describes the laminar flow of a Newtonian fluid through a cylindrical pipe, relating flow rate to pressure difference, pipe dimensions, and fluid viscosity.

Q: Why is the flow rate proportional to the fourth power of the radius?
A: The fourth power relationship (\( r^4 \)) arises from the physics of laminar flow, where the flow rate is highly sensitive to the pipe's radius due to the cross-sectional area and resistance effects.

Q: What are typical applications of Poiseuille's Law?
A: Poiseuille's Law is used in designing medical devices (e.g., IV drips), analyzing blood flow in vessels, and optimizing fluid flow in industrial piping systems.