Pneumatic Cylinder Force Calculator

Cylinder Type:

Piston Diameter (\( D \)):

Rod Diameter (\( d \)):

Pressure (\( P \)):

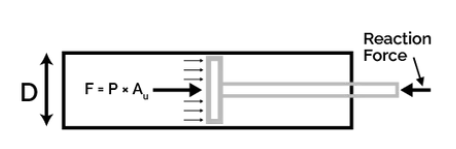
1. What is Pneumatic Cylinder Force Calculator?

Definition: This calculator computes the force exerted by a pneumatic cylinder, based on the cylinder type (single-acting or double-acting), piston diameter (\( D \)), rod diameter (\( d \), for double-acting), pressure (\( P \)), and a fixed friction factor of 10%. For double-acting cylinders, it calculates both the outstroke force (\( F_1 \)) and the return stroke force (\( F_2 \)).

Purpose: It is used in engineering to select the appropriate pneumatic cylinder for applications requiring specific force outputs, such as in automation, robotics, and industrial machinery.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas: For Single-Acting and Double-Acting (Outstroke): \[ F_1 = \left( P \times \left( \frac{\pi}{4} \right) \times D^2 \right) \times 0.9 \] For Double-Acting (Instroke): \[ F_2 = \left( P \times \left( \frac{\pi}{4} \right) \times (D^2 - d^2) \right) \times 0.9 \] Where:

\( F_1 \), \( F_2 \): Force exerted by the cylinder (N, kN, lbf, kgf)
\( P \): Pressure (Pa, kPa, bar, psi)
\( D \): Piston diameter (m, cm, mm, in)
\( d \): Rod diameter (m, cm, mm, in, for double-acting)
0.9: Friction factor (10% friction loss)

Unit Conversions:

Diameter (\( D \), \( d \)):
- 1 m = 1 m
- 1 cm = 0.01 m
- 1 mm = 0.001 m
- 1 in = 0.0254 m
Pressure (\( P \)):
- 1 Pa = 1 Pa
- 1 kPa = 1000 Pa
- 1 bar = 100000 Pa
- 1 psi = 6894.76 Pa
Force (\( F_1 \), \( F_2 \)):
- 1 N = 1 N
- 1 kN = 1000 N
- 1 lbf = 4.44822 N
- 1 kgf = 9.80665 N

Steps:

Select the cylinder type (single-acting or double-acting).
The corresponding image (single-acting or double-acting diagram) will be displayed.
Enter the piston diameter (\( D \)) with its respective unit (m, cm, mm, in).
For double-acting cylinders, enter the rod diameter (\( d \)) with its respective unit.
Enter the pressure (\( P \)) with its respective unit (Pa, kPa, bar, psi).
Convert all inputs to SI units (m for diameters, Pa for pressure).
Calculate the effective areas for outstroke (\( A_1 \)) and instroke (\( A_2 \), for double-acting).
Calculate the outstroke force (\( F_1 \)) and return stroke force (\( F_2 \), for double-acting) using the formulas, applying a 10% friction reduction.
Display the results in the selected force unit, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Pneumatic Cylinder Force Calculation

Calculating pneumatic cylinder force is crucial for:

Cylinder Selection: Ensuring the cylinder provides sufficient force for both outstroke and instroke phases, avoiding undersizing or oversizing.
System Design: Designing efficient pneumatic systems for automation, robotics, and industrial machinery.
Safety: Preventing system failures due to insufficient force or overpressure.

4. Using the Calculator

Examples:

Example 1: Calculate the force exerted by a single-acting cylinder with a piston diameter of 40 mm, pressure of 400 kPa, with force in Newtons:
- Select "Single-Acting" cylinder type (displays single-acting image).
- Enter \( D = 40 \) mm.
- Convert to m: \( D = 40 \times 0.001 = 0.04 \, \text{m} \)
- Enter \( P = 400 \) kPa.
- Convert to Pa: \( P = 400 \times 1000 = 400000 \, \text{Pa} \)
- Area: \( A_1 = \frac{\pi (0.04)^2}{4} = 0.0012566 \, \text{m²} \)
- Outstroke Force: \( F_1 = (400000 \times 0.0012566) \times 0.9 = 452.3893 \, \text{N} \)
- Result: \( F_1 = 452.3893 \, \text{N} \)
Example 2: Calculate the forces exerted by a double-acting cylinder with a piston diameter of 2 in, rod diameter of 0.5 in, pressure of 80 psi, with force in Newtons:
- Select "Double-Acting" cylinder type (displays double-acting image).
- Enter \( D = 2 \) in.
- Convert to m: \( D = 2 \times 0.0254 = 0.0508 \, \text{m} \)
- Enter \( d = 0.5 \) in.
- Convert to m: \( d = 0.5 \times 0.0254 = 0.0127 \, \text{m} \)
- Enter \( P = 80 \) psi.
- Convert to Pa: \( P = 80 \times 6894.76 = 551580.8 \, \text{Pa} \)
- Outstroke Area: \( A_1 = \frac{\pi (0.0508)^2}{4} = 0.002027 \, \text{m²} \)
- Instroke Area: \( A_2 = \frac{\pi (0.0508^2 - 0.0127^2)}{4} = 0.0018965 \, \text{m²} \)
- Outstroke Force: \( F_1 = (551580.8 \times 0.002027) \times 0.9 = 1005.7775 \, \text{N} \)
- Return Stroke Force: \( F_2 = (551580.8 \times 0.0018965) \times 0.9 = 941.4943 \, \text{N} \)
- Result: \( F_1 = 1005.7775 \, \text{N} \), \( F_2 = 941.4943 \, \text{N} \)

5. Frequently Asked Questions (FAQ)

Q: What is the difference between single-acting and double-acting cylinders?
A: Single-acting cylinders use pressurized gas for the outstroke and an external force (e.g., gravity) for the return stroke, while double-acting cylinders use pressurized gas for both outstroke and instroke, requiring a rod diameter input for instroke calculations.

Q: Why is the force reduced by 10%?
A: The 10% reduction accounts for friction losses within the cylinder, as specified in the formulas, ensuring the calculated force reflects a realistic output.

Q: What does the return stroke force (\( F_2 \)) represent?
A: The return stroke force (\( F_2 \)) is the force exerted by a double-acting cylinder during the instroke, accounting for the reduced effective area due to the rod.