Plane Wave Calculator

Relative Permittivity \( \epsilon_r \): ⓘ

Relative Permeability \( \mu_r \): ⓘ

Frequency \( f \): ⓘ

Phase Velocity (\( V_p \)):

Wavelength (\( \lambda \)):

Wave Impedance (\( Z \)):

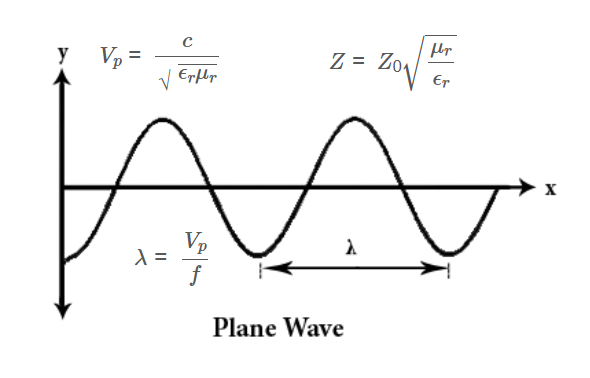
1. What is a Plane Wave?

Definition: A plane wave is an electromagnetic wave where, at any moment, the field values are constant over a plane normal to the direction of propagation. This idealized model is often used in RF and optics to simplify analysis.

Purpose: This calculator determines key properties of a plane wave in a medium, such as phase velocity, wavelength, and wave impedance, which are essential for RF system design, wave propagation studies, and material characterization.

2. How Does the Calculator Work?

The calculator uses the following formulas for a plane wave in a medium:

Phase Velocity: \[ V_p = \frac{c}{\sqrt{\epsilon_r \mu_r}} \]

Wavelength: \[ \lambda = \frac{V_p}{f} \]

Wave Impedance: \[ Z = Z_0 \sqrt{\frac{\mu_r}{\epsilon_r}} \]

Where:

\( V_p \): Phase velocity in m/s
\( \lambda \): Wavelength in meters
\( Z \): Wave impedance in ohms (\( \Omega \))
\( \epsilon_r \): Relative permittivity of the medium
\( \mu_r \): Relative permeability of the medium
\( f \): Frequency (converted to Hz from MHz or GHz)
\( c \): Speed of light (\( 3 \times 10^8 \, \text{m/s} \))
\( Z_0 \): Impedance of free space (\( 376.73 \, \Omega \))

Steps:

Enter the relative permittivity \( \epsilon_r \) and relative permeability \( \mu_r \) of the medium.
Enter the frequency \( f \) and select its unit (MHz, GHz).
Click "Calculate" to compute the phase velocity, wavelength, and wave impedance.
Results are displayed in m/s, meters, and ohms, respectively.

3. Importance of Plane Wave Properties

Plane wave properties are crucial for:

Wave Propagation: Understanding how waves travel through different media in RF systems.
Material Characterization: Determining the electromagnetic properties of materials using \(\epsilon_r\) and \(\mu_r\).
Antenna Design: Calculating wavelengths and impedances for antenna matching and performance optimization.

4. Using the Calculator

Examples:

Example 1: Free Space
- \( \epsilon_r = 1, \mu_r = 1, f = 1 \, \text{GHz} \)
- \( V_p = \frac{3 \times 10^8}{\sqrt{1 \times 1}} = 3 \times 10^8 \, \text{m/s} \)
- \( \lambda = \frac{3 \times 10^8}{1 \times 10^9} = 0.30 \, \text{m} \)
- \( Z = 376.73 \times \sqrt{\frac{1}{1}} = 376.73 \, \Omega \)
Example 2: Dielectric Medium
- \( \epsilon_r = 4, \mu_r = 1, f = 100 \, \text{MHz} \)
- \( V_p = \frac{3 \times 10^8}{\sqrt{4 \times 1}} = 1.5 \times 10^8 \, \text{m/s} \)
- \( \lambda = \frac{1.5 \times 10^8}{100 \times 10^6} = 1.50 \, \text{m} \)
- \( Z = 376.73 \times \sqrt{\frac{1}{4}} = 188.37 \, \Omega \)
Example 3: Magnetic Medium
- \( \epsilon_r = 1, \mu_r = 2, f = 2 \, \text{GHz} \)
- \( V_p = \frac{3 \times 10^8}{\sqrt{1 \times 2}} \approx 2.12 \times 10^8 \, \text{m/s} \)
- \( \lambda = \frac{2.12 \times 10^8}{2 \times 10^9} \approx 0.11 \, \text{m} \)
- \( Z = 376.73 \times \sqrt{\frac{2}{1}} \approx 532.81 \, \Omega \)

5. Frequently Asked Questions (FAQ)

Q: What is a plane wave?
A: A plane wave is an electromagnetic wave where the field values are constant over a plane normal to the direction of propagation, often used as a simplified model in RF and optics.

Q: Why are \(\epsilon_r\) and \(\mu_r\) important?
A: The relative permittivity (\(\epsilon_r\)) and permeability (\(\mu_r\)) determine how electromagnetic waves propagate in a medium, affecting velocity, wavelength, and impedance.

Q: How does frequency affect wavelength?
A: Wavelength (\(\lambda\)) is inversely proportional to frequency (\(f\)) through the phase velocity (\(\lambda = V_p / f\)). Higher frequencies result in shorter wavelengths.