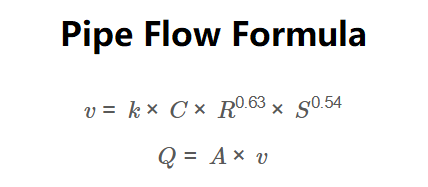1. What is Pipe Flow Calculator?
Definition: This calculator computes the flow velocity (\( v \)) and flow discharge (\( Q \)) of gravity flow in a pipe using the Manning formula, based on the pipe diameter (\( d \)), roughness coefficient (\( C \)), pipe length (\( L \)), and drop (\( \Delta h \)).
Purpose: It is used in civil engineering and fluid mechanics to determine the flow characteristics in open channels, sewers, and pipelines, aiding in the design and analysis of water distribution systems.
2. How Does the Calculator Work?
The calculator uses the following formulas:
Formulas:
\[
v = k \times C \times R^{0.63} \times S^{0.54}
\]
\[
Q = A \times v
\]
\[
S = \frac{\Delta h}{L}
\]
Where:
- \( v \): Flow velocity (m/s, ft/s, km/h, mph)
- \( k \): Conversion factor (\( k = 0.849 \), using metric internally)
- \( C \): Roughness coefficient (Manning's \( n \), dimensionless)
- \( R \): Hydraulic radius (m), calculated as \( R = \frac{r}{2} \) for a full circular pipe, where \( r \) is the radius
- \( S \): Slope of the energy line (dimensionless), calculated as \( S = \frac{\Delta h}{L} \)
- \( \Delta h \): Drop (m, cm, mm, ft, in)
- \( L \): Pipe length (m, cm, mm, ft, in)
- \( Q \): Flow discharge (m³/s, L/s, m³/min, ft³/s, ft³/min)
- \( A \): Cross-sectional area of the pipe (m²), calculated as \( A = \pi r^2 \), where \( r \) is the radius
Predefined Roughness Coefficients:
- Cast Iron: \( C = 100 \)
- Concrete: \( C = 110 \)
- Copper: \( C = 140 \)
- Plastic: \( C = 150 \)
- Steel: \( C = 120 \)
Unit Conversions:
- Diameter (\( d \)), Length (\( L \)), and Drop (\( \Delta h \)):
- 1 m = 1 m
- 1 cm = 0.01 m
- 1 mm = 0.001 m
- 1 ft = 0.3048 m
- 1 in = 0.0254 m
- Velocity (\( v \)):
- 1 m/s = 1 m/s
- 1 ft/s = 0.3048 m/s
- 1 km/h = 0.277778 m/s
- 1 mph = 0.44704 m/s
- Flow Discharge (\( Q \)):
- 1 m³/s = 1 m³/s
- 1 L/s = 0.001 m³/s
- 1 m³/min = \( \frac{1}{60} \) m³/s
- 1 ft³/s = \( (0.3048)^3 \) m³/s
- 1 ft³/min = \( \frac{(0.3048)^3}{60} \) m³/s
Steps:
- Select the pipe material from the dropdown or choose "Custom" to enter your own roughness coefficient.
- If a predefined material is selected, the roughness coefficient field will auto-fill and become read-only.
- Enter the pipe diameter (\( d \)) with its respective unit (m, cm, mm, ft, in).
- Enter the pipe length (\( L \)) with its respective unit (m, cm, mm, ft, in).
- Enter the drop (\( \Delta h \)) with its respective unit (m, cm, mm, ft, in).
- Convert all inputs to meters for calculation.
- Calculate the slope using \( S = \frac{\Delta h}{L} \).
- Calculate the radius (\( r = d/2 \)), area (\( A = \pi r^2 \)), and hydraulic radius (\( R = r/2 \)).
- Calculate the velocity using \( v = k \times C \times R^{0.63} \times S^{0.54} \).
- Calculate the flow discharge using \( Q = A \times v \).
- Display the velocity and flow discharge in the selected units, using scientific notation for values less than 0.001, otherwise with 4 decimal places.
3. Importance of Pipe Flow Calculation
Calculating pipe flow is crucial for:
- Water Distribution: Designing efficient pipelines for water supply, irrigation, and drainage systems.
- Sewer Design: Ensuring proper flow in sewer systems to prevent blockages and overflows.
- Hydraulic Engineering: Analyzing flow characteristics in open channels and conduits for infrastructure projects.
4. Using the Calculator
Examples:
- Example 1: Calculate the flow velocity and discharge in a cast iron pipe with a diameter of 300 mm, length of 100 m, drop of 1 m, with velocity in m/s and discharge in m³/s:
- Select "Cast Iron" (auto-fills \( C = 100 \)).
- Enter \( d = 300 \) mm.
- Convert to m: \( d = 300 \times 0.001 = 0.3 \, \text{m} \)
- Enter \( L = 100 \) m.
- Enter \( \Delta h = 1 \) m.
- Slope: \( S = \frac{1}{100} = 0.01 \)
- Radius: \( r = 0.3 / 2 = 0.15 \, \text{m} \)
- Area: \( A = \pi (0.15)^2 = 0.0707 \, \text{m²} \)
- Hydraulic radius: \( R = 0.15 / 2 = 0.075 \, \text{m} \)
- Velocity: \( v = 0.849 \times 100 \times (0.075)^{0.63} \times (0.01)^{0.54} = 1.1738 \, \text{m/s} \)
- Flow discharge: \( Q = 0.0707 \times 1.1738 = 0.0830 \, \text{m³/s} \)
- Result: \( v = 1.1738 \, \text{m/s} \), \( Q = 0.0830 \, \text{m³/s} \)
- Example 2: Calculate the flow velocity and discharge in a plastic pipe with a diameter of 1 ft, length of 500 ft, drop of 10 ft, with velocity in ft/s and discharge in ft³/s:
- Select "Plastic" (auto-fills \( C = 150 \)).
- Enter \( d = 1 \) ft.
- Convert to m: \( d = 1 \times 0.3048 = 0.3048 \, \text{m} \)
- Enter \( L = 500 \) ft.
- Convert to m: \( L = 500 \times 0.3048 = 152.4 \, \text{m} \)
- Enter \( \Delta h = 10 \) ft.
- Convert to m: \( \Delta h = 10 \times 0.3048 = 3.048 \, \text{m} \)
- Slope: \( S = \frac{3.048}{152.4} = 0.02 \)
- Radius: \( r = 0.3048 / 2 = 0.1524 \, \text{m} \)
- Area: \( A = \pi (0.1524)^2 = 0.0729 \, \text{m²} \)
- Hydraulic radius: \( R = 0.1524 / 2 = 0.0762 \, \text{m} \)
- Velocity: \( v = 0.849 \times 150 \times (0.0762)^{0.63} \times (0.02)^{0.54} = 1.6146 \, \text{m/s} \)
- Convert to ft/s: \( v = 1.6146 / 0.3048 = 5.2972 \, \text{ft/s} \)
- Flow discharge: \( Q = 0.0729 \times 1.6146 = 0.1177 \, \text{m³/s} \)
- Convert to ft³/s: \( Q = 0.1177 / (0.3048)^3 = 4.1567 \, \text{ft³/s} \)
- Result: \( v = 5.2972 \, \text{ft/s} \), \( Q = 4.1567 \, \text{ft³/s} \)
5. Frequently Asked Questions (FAQ)
Q: What is the roughness coefficient (\( C \))?
A: The roughness coefficient (\( C \)), also known as Manning's \( n \), represents the frictional resistance of the pipe material. Higher values indicate smoother pipes (e.g., plastic: 150), while lower values indicate rougher pipes (e.g., cast iron: 100).
Q: What does the drop (\( \Delta h \)) represent?
A: The drop (\( \Delta h \)) is the vertical elevation difference over the pipe length, used to calculate the slope (\( S \)) that drives the gravity flow.
Q: Can this calculator be used for partially filled pipes?
A: This calculator assumes the pipe is flowing full. For partially filled pipes, the hydraulic radius and area would need to be adjusted, which requires a more complex calculation.
 Home
Home
 Back
Back