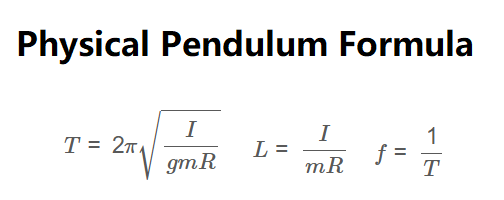1. What is a Physical Pendulum Calculator?

Definition: This calculator computes the period (\( T \)), equivalent length (\( L \)), and frequency (\( f \)) of a physical pendulum based on its moment of inertia, mass, distance from the center of mass to the pivot, and the acceleration due to gravity.

Purpose: It is used in physics to analyze the oscillatory motion of a physical pendulum, which differs from a simple pendulum by having a distributed mass rather than a point mass.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Period: \[ T = 2\pi \sqrt{\frac{I}{g m R}} \] Equivalent Length: \[ L = \frac{I}{m R} \] Frequency: \[ f = \frac{1}{T} \] Where:

• \( T \): Period (sec, min, hr)
• \( L \): Equivalent length (mm, cm, m, in, ft, yd)
• \( f \): Frequency (Hz, kHz, MHz)
• \( I \): Moment of inertia (kg·m², kg·cm², g·cm²)
• \( g \): Acceleration due to gravity (m/s², ft/s²)
• \( m \): Mass (mg, g, dag, kg, oz, lb, st)
• \( R \): Distance from center of mass to pivot (mm, cm, m, in, ft, yd)

Unit Conversions:

• Moment of Inertia (\( I \)): kg·m², kg·cm² (1 kg·m² = 10000 kg·cm²), g·cm² (1 kg·m² = 100000 g·cm²)
• Mass (\( m \)): mg (1 mg = 0.000001 kg), g (1 g = 0.001 kg), dag (1 dag = 0.01 kg), kg, oz (1 oz = 0.028349523125 kg), lb (1 lb = 0.45359237 kg), st (1 st = 6.35029318 kg)
• Distance (\( R \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
• Acceleration due to Gravity (\( g \)): m/s², ft/s² (1 ft/s² = 0.3048 m/s²)
• Period (\( T \)): sec, min (1 min = 60 sec), hr (1 hr = 3600 sec)
• Equivalent Length (\( L \)): mm (1 m = 1000 mm), cm (1 m = 100 cm), m, in (1 m = 39.3701 in), ft (1 m = 3.28084 ft), yd (1 m = 1.09361 yd)
• Frequency (\( f \)): Hz, kHz (1 Hz = 0.001 kHz), MHz (1 Hz = 0.000001 MHz)

Steps:

• Enter the moment of inertia, mass, distance from the center of mass to the pivot, and acceleration due to gravity, and select their units.
• Convert all inputs to base units (kg·m² for moment, kg for mass, m for distance, m/s² for gravity).
• Calculate the equivalent length, period, and frequency using the provided formulas.
• Convert the results to the selected units.
• Display the results, using scientific notation for values less than 0.001, otherwise with 3 decimal places.

3. Importance of Physical Pendulum Calculation

Calculating the period, equivalent length, and frequency of a physical pendulum is crucial for:

• Physics Education: Understanding the principles of rotational dynamics and oscillatory motion.
• Engineering Applications: Designing systems involving rotational motion, such as clocks, seismometers, or mechanical oscillators.
• Scientific Research: Analyzing the motion of complex pendulums in experimental setups.

4. Using the Calculator

Examples:

• Example 1: For \( I = 0.1 \, \text{kg·m}^2 \), \( m = 2 \, \text{kg} \), \( R = 0.5 \, \text{m} \), \( g = 9.81 \, \text{m/s}^2 \), period in sec, length in m, frequency in Hz:
  • Equivalent Length: \( L = \frac{0.1}{2 \times 0.5} = 0.1 \, \text{m} \)
  • Period: \( T = 2 \pi \sqrt{\frac{0.1}{9.81 \times 2 \times 0.5}} = 2 \pi \sqrt{\frac{0.1}{9.81}} = 2 \pi \times 0.1009 = 0.634 \, \text{sec} \)
  • Frequency: \( f = \frac{1}{0.634} = 1.577 \, \text{Hz} \)
• Example 2: For \( I = 1000 \, \text{g·cm}^2 \), \( m = 500 \, \text{g} \), \( R = 20 \, \text{cm} \), \( g = 32.17405 \, \text{ft/s}^2 \), period in sec, length in cm, frequency in Hz:
  • Convert: \( I = 1000 \times 0.00001 = 0.01 \, \text{kg·m}^2 \), \( m = 500 \times 0.001 = 0.5 \, \text{kg} \), \( R = 20 \times 0.01 = 0.2 \, \text{m} \), \( g = 32.17405 \times 0.3048 = 9.81 \, \text{m/s}^2 \)
  • Equivalent Length: \( L = \frac{0.01}{0.5 \times 0.2} = 0.1 \, \text{m} = 0.1 \times 100 = 10 \, \text{cm} \)
  • Period: \( T = 2 \pi \sqrt{\frac{0.01}{9.81 \times 0.5 \times 0.2}} = 2 \pi \sqrt{\frac{0.01}{0.981}} = 2 \pi \times 0.1009 = 0.634 \, \text{sec} \)
  • Frequency: \( f = \frac{1}{0.634} = 1.577 \, \text{Hz} \)

5. Frequently Asked Questions (FAQ)

Q: What is a physical pendulum?
A: A physical pendulum is a rigid body that oscillates about a pivot point under the influence of gravity, unlike a simple pendulum which assumes a point mass.

Q: How does a physical pendulum differ from a simple pendulum?
A: A physical pendulum has a distributed mass with a moment of inertia, while a simple pendulum assumes a point mass at the end of a massless string. The period of a physical pendulum depends on its moment of inertia and the distance from the pivot to the center of mass.

Q: What is the equivalent length \( L \)?
A: The equivalent length \( L \) is the length of a simple pendulum that would have the same period as the physical pendulum, given by \( L = \frac{I}{m R} \).

Physical Pendulum Calculator© - All Rights Reserved 2025