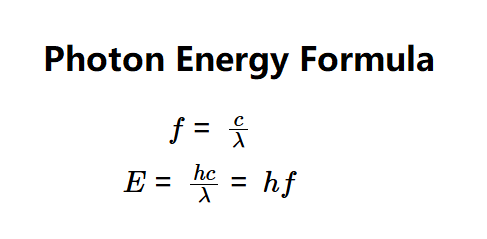Photon Energy Calculator

Frequency (\( f \)):

Energy (\( E \)):

1. What is the Photon Energy Calculator?

Definition: This calculator computes the frequency (\( f \)) and energy (\( E \)) of a photon based on its wavelength (\( \lambda \)) using Planck's photon energy equation.

Purpose: It is used in quantum physics to determine the energy of a photon, which is essential for understanding phenomena like the photoelectric effect, atomic transitions, and the interaction of light with matter.

2. How Does the Calculator Work?

The calculator uses the following equations:

\( f = \frac{c}{\lambda} \)
\( E = \frac{h c}{\lambda} = h f \)

Where:

\( \lambda \): Wavelength (m, cm, mm, nm, pm, Å);
\( f \): Frequency (Hz, kHz, MHz, GHz, THz);
\( E \): Energy (J, neV, µeV, meV, eV, keV, MeV);
\( c \): Speed of light (\( 299,792,458 \, \text{m/s} \));
\( h \): Planck constant (\( 6.626 \times 10^{-34} \, \text{J·s} \)).

Steps:

Enter the wavelength (\( \lambda \)) with its unit.
Convert the wavelength to meters.
Calculate the frequency: \( f = \frac{c}{\lambda} \).
Calculate the energy: \( E = \frac{h c}{\lambda} \).
Convert the frequency and energy to the selected output units and display, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Photon Energy Calculation

Calculating the energy of a photon is crucial for:

Quantum Physics: Understanding the particle nature of light and photon interactions with matter.
Spectroscopy: Analyzing the energy of photons emitted or absorbed during atomic transitions.
Technology: Applications in lasers, photodetectors, and solar cells, where photon energy determines functionality.

4. Using the Calculator

Example 1: Calculate the frequency and energy of a photon with a wavelength of 500 nm (visible light):

Wavelength: \( \lambda = 500 \, \text{nm} = 5 \times 10^{-7} \, \text{m} \);
Frequency: \( f = \frac{299,792,458}{5 \times 10^{-7}} \approx 5.996 \times 10^{14} \, \text{Hz} \approx 599.6 \, \text{THz} \);
Energy: \( E = \frac{6.626 \times 10^{-34} \times 299,792,458}{5 \times 10^{-7}} \approx 3.976 \times 10^{-19} \, \text{J} \approx 2.482 \, \text{eV} \);
Result: \( f = 599.6000 \, \text{THz} \), \( E = 2.4820 \, \text{eV} \).

Example 2 (X-ray Photon): Calculate the frequency and energy of a photon with a wavelength of 1 Å (X-ray):

Wavelength: \( \lambda = 1 \, \text{Å} = 1 \times 10^{-10} \, \text{m} \);
Frequency: \( f = \frac{299,792,458}{1 \times 10^{-10}} \approx 2.998 \times 10^{18} \, \text{Hz} \approx 2.998 \times 10^6 \, \text{THz} \);
Energy: \( E = \frac{6.626 \times 10^{-34} \times 299,792,458}{1 \times 10^{-10}} \approx 1.986 \times 10^{-15} \, \text{J} \approx 12.398 \, \text{keV} \);
Result: \( f = 2.9980 \times 10^6 \, \text{THz} \), \( E = 12.3980 \, \text{keV} \).

5. Frequently Asked Questions (FAQ)

Q: What does the energy of a photon tell us?
A: The energy of a photon determines its ability to interact with matter, such as ejecting electrons (photoelectric effect) or exciting atomic transitions, and it defines the photon's place in the electromagnetic spectrum.

Q: Why does a shorter wavelength result in higher energy?
A: Energy is inversely proportional to wavelength (\( E \propto \frac{1}{\lambda} \)). A shorter wavelength means a higher frequency (\( f \propto \frac{1}{\lambda} \)), and since \( E = h f \), the energy increases.

Q: Can this calculator be used for photons in a medium?
A: This calculator assumes photons travel in a vacuum (\( c = 299,792,458 \, \text{m/s} \)). In a medium, the speed of light is slower, and the equation would need adjustment (\( E = \frac{h v}{\lambda} \), where \( v \) is the speed in the medium).