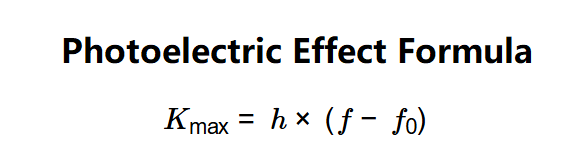Photoelectric Effect Calculator

Frequency of Incident Photon (\( f \)):

Threshold Frequency (\( f_0 \)):

Wavelength (\( \lambda \)):

Threshold Wavelength (\( \lambda_0 \)):

Wave Energy (\( E \)):

Threshold Energy (\( E_0 \)):

Maximum Kinetic Energy (\( K_{\text{max}} \)):

1. What is the Photoelectric Effect Calculator?

Definition: This calculator uses the photoelectric effect equation to compute the wavelength (\( \lambda \)), threshold wavelength (\( \lambda_0 \)), wave energy (\( E \)), threshold energy (\( E_0 \)), and maximum kinetic energy (\( K_{\text{max}} \)) of an ejected electron based on the frequency of the incident photon (\( f \)) and the threshold frequency (\( f_0 \)).

Purpose: It is used in quantum physics to study the photoelectric effect, which describes how photons eject electrons from a material, providing insight into the particle nature of light and the energy required to overcome the material's work function.

2. How Does the Calculator Work?

The calculator uses the following equations:

\( \lambda = \frac{c}{f} \)
\( \lambda_0 = \frac{c}{f_0} \)
\( E = h \times f \)
\( E_0 = h \times f_0 \)
\( K_{\text{max}} = h \times (f - f_0) \)

Where:

\( \lambda \), \( \lambda_0 \): Wavelength and threshold wavelength (m, cm, mm, nm, pm, Å);
\( E \), \( E_0 \), \( K_{\text{max}} \): Wave energy, threshold energy, and maximum kinetic energy (J, neV, µeV, meV, eV, keV, MeV);
\( f \), \( f_0 \): Frequency and threshold frequency (Hz, kHz, MHz, GHz, THz);
\( c \): Speed of light (\( 299,792,458 \, \text{m/s} \));
\( h \): Planck constant (\( 6.626 \times 10^{-34} \, \text{J·s} \)).

Steps:

Enter the frequency of the incident photon (\( f \)) with its unit.
Enter the threshold frequency (\( f_0 \)) with its unit.
Convert the frequencies to Hz.
Calculate the wavelength: \( \lambda = \frac{c}{f} \).
Calculate the threshold wavelength: \( \lambda_0 = \frac{c}{f_0} \).
Calculate the wave energy: \( E = h \times f \).
Calculate the threshold energy: \( E_0 = h \times f_0 \).
Calculate the maximum kinetic energy: \( K_{\text{max}} = h \times (f - f_0) \), or 0 if \( f < f_0 \).
Convert the results to the selected output units and display, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Photoelectric Effect Calculation

Calculating the photoelectric effect parameters is crucial for:

Quantum Physics: Validating the particle nature of light and the concept of photons.
Material Science: Determining the work function of materials.
Technology: Applications in photodetectors, solar cells, and other devices that rely on the photoelectric effect.

4. Using the Calculator

Example 1: Calculate the photoelectric effect parameters for a photon incident on a metal with a threshold frequency:

Frequency: \( f = 600 \, \text{THz} = 6 \times 10^{14} \, \text{Hz} \);
Threshold Frequency: \( f_0 = 400 \, \text{THz} = 4 \times 10^{14} \, \text{Hz} \);
Wavelength: \( \lambda = \frac{299,792,458}{6 \times 10^{14}} \approx 499.654 \, \text{nm} \);
Threshold Wavelength: \( \lambda_0 = \frac{299,792,458}{4 \times 10^{14}} \approx 749.481 \, \text{nm} \);
Wave Energy: \( E = 6.626 \times 10^{-34} \times 6 \times 10^{14} \approx 3.976 \times 10^{-19} \, \text{J} \approx 2.482 \, \text{eV} \);
Threshold Energy: \( E_0 = 6.626 \times 10^{-34} \times 4 \times 10^{14} \approx 2.650 \times 10^{-19} \, \text{J} \approx 1.655 \, \text{eV} \);
Maximum Kinetic Energy: \( K_{\text{max}} = 6.626 \times 10^{-34} \times (6 \times 10^{14} - 4 \times 10^{14}) \approx 1.325 \times 10^{-19} \, \text{J} \approx 0.827 \, \text{eV} \);
Result: \( \lambda = 499.6540 \, \text{nm} \), \( \lambda_0 = 749.4810 \, \text{nm} \), \( E = 2.4820 \, \text{eV} \), \( E_0 = 1.6550 \, \text{eV} \), \( K_{\text{max}} = 0.8270 \, \text{eV} \).

Example 2 (Below Threshold): Calculate the photoelectric effect parameters when the frequency is below the threshold:

Frequency: \( f = 300 \, \text{THz} = 3 \times 10^{14} \, \text{Hz} \);
Threshold Frequency: \( f_0 = 400 \, \text{THz} = 4 \times 10^{14} \, \text{Hz} \);
Wavelength: \( \lambda = \frac{299,792,458}{3 \times 10^{14}} \approx 999.308 \, \text{nm} \);
Threshold Wavelength: \( \lambda_0 = \frac{299,792,458}{4 \times 10^{14}} \approx 749.481 \, \text{nm} \);
Wave Energy: \( E = 6.626 \times 10^{-34} \times 3 \times 10^{14} \approx 1.988 \times 10^{-19} \, \text{J} \approx 1.241 \, \text{eV} \);
Threshold Energy: \( E_0 = 6.626 \times 10^{-34} \times 4 \times 10^{14} \approx 2.650 \times 10^{-19} \, \text{J} \approx 1.655 \, \text{eV} \);
Maximum Kinetic Energy: \( K_{\text{max}} = 0 \, \text{(since } f < f_0\text{)} \);
Result: \( \lambda = 999.3080 \, \text{nm} \), \( \lambda_0 = 749.4810 \, \text{nm} \), \( E = 1.2410 \, \text{eV} \), \( E_0 = 1.6550 \, \text{eV} \), \( K_{\text{max}} = 0.0000 \, \text{eV} \).

5. Frequently Asked Questions (FAQ)

Q: What does the threshold frequency represent?
A: The threshold frequency (\( f_0 \)) is the minimum frequency required for a photon to eject an electron from a material, corresponding to the material's work function.

Q: Why is the maximum kinetic energy zero when the frequency is below the threshold?
A: If the photon's frequency (\( f \)) is less than the threshold frequency (\( f_0 \)), the photon does not have enough energy to overcome the material's work function, so no electron is ejected, and \( K_{\text{max}} = 0 \).

Q: Can this calculator be used for any material?
A: Yes, as long as you know the threshold frequency (\( f_0 \)) of the material, which is related to its work function. Different materials have different \( f_0 \) values.