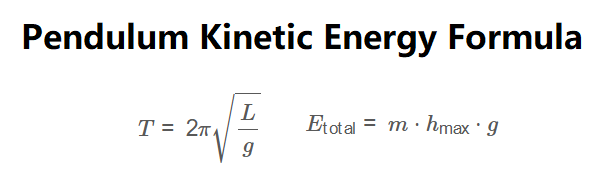1. What is a Pendulum Kinetic Energy Calculator?

Definition: This calculator computes the period (\( T \)) and the kinetic energy (\( E_{\text{kinetic}} \)) at the lowest point of a pendulum’s swing, based on its length, mass, maximum height, and the acceleration due to gravity.

Purpose: It is used in physics to analyze the motion and energy of a simple pendulum, helping to understand the conservation of mechanical energy in oscillatory systems.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Period: \[ T = 2\pi \sqrt{\frac{L}{g}} \] Total Energy (Maximum Potential Energy): \[ E_{\text{total}} = m \cdot h_{\text{max}} \cdot g \] Kinetic Energy at Lowest Point: \[ E_{\text{kinetic}} = E_{\text{total}} \] Where:

• \( T \): Period (sec, min, hr)
• \( L \): Length of the pendulum (mm, cm, m, in, ft, yd)
• \( g \): Acceleration due to gravity (m/s², ft/s²)
• \( E_{\text{total}} \): Total energy (J, kJ, MJ, Wh)
• \( E_{\text{kinetic}} \): Kinetic energy at the lowest point (J, kJ, MJ, Wh)
• \( m \): Mass (mg, g, dag, kg, oz, lb, st, Earth)
• \( h_{\text{max}} \): Maximum height (mm, cm, m, in, ft, yd)

Unit Conversions:

• Length (\( L \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
• Mass (\( m \)): mg (1 mg = 0.000001 kg), g (1 g = 0.001 kg), dag (1 dag = 0.01 kg), kg, oz (1 oz = 0.028349523125 kg), lb (1 lb = 0.45359237 kg), st (1 st = 6.35029318 kg), Earth (1 Earth = 5.972 × 10²⁴ kg)
• Maximum Height (\( h_{\text{max}} \)): mm (1 mm = 0.001 m), cm (1 cm = 0.01 m), m, in (1 in = 0.0254 m), ft (1 ft = 0.3048 m), yd (1 yd = 0.9144 m)
• Acceleration due to Gravity (\( g \)): m/s², ft/s² (1 ft/s² = 0.3048 m/s²)
• Period (\( T \)): sec, min (1 min = 60 sec), hr (1 hr = 3600 sec)
• Kinetic Energy (\( E_{\text{kinetic}} \)): J, kJ (1 kJ = 1000 J), MJ (1 MJ = 1000000 J), Wh (1 Wh = 3600 J)

Steps:

• Enter the length, mass, maximum height, and acceleration due to gravity, and select their units.
• Convert all inputs to base units (m for lengths, kg for mass, m/s² for gravity).
• Calculate the period and kinetic energy using the provided formulas.
• Convert the results to the selected units.
• Display the results, using scientific notation for values less than 0.001, otherwise with 3 decimal places.

3. Importance of Pendulum Kinetic Energy Calculation

Calculating the period and kinetic energy of a pendulum is crucial for:

• Physics Education: Understanding the principles of simple harmonic motion and energy conservation.
• Engineering Applications: Designing pendulum-based systems, such as clocks or seismometers.
• Energy Analysis: Analyzing the energy transformations in oscillatory systems.

4. Using the Calculator

Examples:

• Example 1: For \( L = 1 \, \text{m} \), \( m = 2 \, \text{kg} \), \( h_{\text{max}} = 0.1 \, \text{m} \), \( g = 9.80665 \, \text{m/s}^2 \), period in sec, kinetic energy in J:
  • Period: \( T = 2 \pi \sqrt{\frac{1}{9.80665}} = 2 \pi \times 0.3194 = 2.006 \, \text{sec} \)
  • Kinetic Energy: \( E_{\text{kinetic}} = 2 \times 0.1 \times 9.80665 = 1.961 \, \text{J} \)
• Example 2: For \( L = 50 \, \text{cm} \), \( m = 500 \, \text{g} \), \( h_{\text{max}} = 10 \, \text{cm} \), \( g = 32.17405 \, \text{ft/s}^2 \), period in sec, kinetic energy in kJ:
  • Convert: \( L = 50 \times 0.01 = 0.5 \, \text{m} \), \( m = 500 \times 0.001 = 0.5 \, \text{kg} \), \( h_{\text{max}} = 10 \times 0.01 = 0.1 \, \text{m} \), \( g = 32.17405 \times 0.3048 = 9.80665 \, \text{m/s}^2 \)
  • Period: \( T = 2 \pi \sqrt{\frac{0.5}{9.80665}} = 2 \pi \times 0.2258 = 1.419 \, \text{sec} \)
  • Kinetic Energy: \( E_{\text{kinetic}} = 0.5 \times 0.1 \times 9.80665 = 0.4903 \, \text{J} \), \( E_{\text{kinetic}} = 0.4903 \times 0.001 = 0.000 \, \text{kJ} \) (displayed as \( 4.903 \times 10^{-4} \, \text{kJ} \))

5. Frequently Asked Questions (FAQ)

Q: What is a pendulum?
A: A pendulum is a mass (bob) suspended from a pivot point by a string or rod, which oscillates under the influence of gravity, often used to demonstrate simple harmonic motion.

Q: Why does the period depend only on length and gravity?
A: For small angles, the period of a simple pendulum is independent of mass and amplitude, depending only on the length (\( L \)) and gravity (\( g \)), as shown in the formula \( T = 2\pi \sqrt{\frac{L}{g}} \).

Q: What does the kinetic energy at the lowest point represent?
A: At the lowest point, all the pendulum’s potential energy is converted to kinetic energy, representing the maximum kinetic energy during the swing, equal to the total energy of the system.

Pendulum Kinetic Energy Calculator© - All Rights Reserved 2025