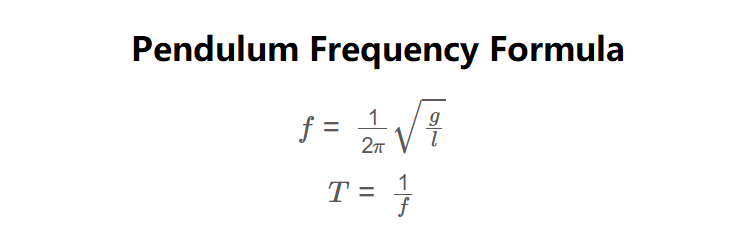1. What is the Pendulum Frequency Calculator?

Definition: This calculator computes the frequency (\( f \)) and period (\( T \)) of oscillation of a simple pendulum based on its length (\( l \)) and the gravitational acceleration (\( g \)).

Purpose: It is used in physics and engineering to analyze the oscillatory behavior of pendulums, such as in clocks or seismometers.

2. How Does the Calculator Work?

The calculator uses the formula:

\( f = \frac{1}{2\pi} \sqrt{\frac{g}{l}} \)

\( T = \frac{1}{f} \)

Where:

• \( f \): Frequency (Hz, kHz, MHz, GHz);
• \( T \): Period (s, min, hrs);
• \( g \): Gravitational acceleration (m/s², ft/s²);
• \( l \): Length of the pendulum (m, cm, mm, ft, in).

Steps:

• Enter the pendulum length (\( l \)) with its unit.
• Enter the gravitational acceleration (\( g \)) with its unit (optional, defaults to 9.81 m/s²).
• Convert length to meters and gravity to m/s².
• Calculate the frequency using \( f = \frac{1}{2\pi} \sqrt{\frac{g}{l}} \).
• Calculate the period using \( T = \frac{1}{f} \).
• Convert the results to the selected output units.
• Display the results, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Pendulum Frequency and Period Calculation

Calculating the frequency and period of a pendulum is crucial for:

• Physics Education: Understanding oscillatory motion.
• Timekeeping: Designing accurate pendulum clocks.
• Engineering:** Analyzing dynamic systems like seismographs.

4. Using the Calculator

Example 1: Calculate the frequency and period with \( l = 1 \, \text{m} \), \( g = 9.81 \, \text{m/s}^2 \):

• Length: \( l = 1 \, \text{m} \);
• Gravitational Acceleration: \( g = 9.81 \, \text{m/s}^2 \);
• Frequency: \( f = \frac{1}{2\pi} \sqrt{\frac{9.81}{1}} \approx 0.4979 \, \text{Hz} \);
• Period: \( T = \frac{1}{0.4979} \approx 2.0078 \, \text{s} \);
• Result (Frequency in Hz): \( f = 0.4979 \, \text{Hz} \);
• Result (Period in s): \( T = 2.0078 \, \text{s} \).

Example 2: Calculate the frequency and period with \( l = 50 \, \text{cm} \), \( g = 32.174 \, \text{ft/s}^2 \):

• Length: \( l = 50 \, \text{cm} \times 0.01 = 0.5 \, \text{m} \);
• Gravitational Acceleration: \( g = 32.174 \, \text{ft/s}^2 \times 0.3048 \approx 9.807 \, \text{m/s}^2 \);
• Frequency: \( f = \frac{1}{2\pi} \sqrt{\frac{9.807}{0.5}} \approx 0.7045 \, \text{Hz} \);
• Period: \( T = \frac{1}{0.7045} \approx 1.4191 \, \text{s} \);
• Result (Frequency in kHz): \( f = 0.0007 \, \text{kHz} \);
• Result (Period in min): \( T = 0.0237 \, \text{min} \).

5. Frequently Asked Questions (FAQ)

Q: What is the frequency of a pendulum?
A: The frequency (\( f \)) is the number of oscillations per second, determined by the pendulum's length and local gravity.

Q: What is the period of a pendulum?
A: The period (\( T \)) is the time for one complete oscillation, the inverse of the frequency.

Q: Does this calculator account for air resistance?
A: No, this calculator assumes an ideal pendulum with no air resistance or friction.