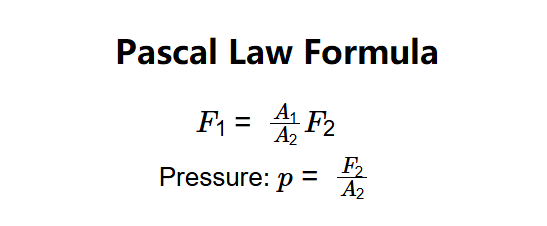Pascal's Law Calculator

Area of First Piston (\( A_1 \)):

Area of Second Piston (\( A_2 \)):

Force on Second Piston (\( F_2 \)):

Force on First Piston (\( F_1 \)):

Force on Second Piston (\( F_2 \)):

Hydraulic Pressure (\( p \)):

1. What is Pascal's Law Calculator?

Definition: This calculator computes the forces and pressure in a hydraulic system using Pascal's law, based on the areas of the first and second pistons and the force applied to the second piston.

Purpose: It is used in engineering to analyze hydraulic systems, such as lifts and presses, by determining the force required on one piston given the force on another and the piston areas.

2. How Does the Calculator Work?

The calculator uses Pascal's law in the form provided:

\( F_1 = \frac{A_1}{A_2} F_2 \)
Pressure: \( p = \frac{F_2}{A_2} \)

Where:

\( A_1 \): Area of the first piston (m²);
\( A_2 \): Area of the second piston (m²);
\( F_1 \): Force on the first piston (N, converted to selected unit);
\( F_2 \): Force on the second piston (N, converted to selected unit);
\( p \): Hydraulic pressure (Pa, converted to selected unit).

Steps:

Enter the area of the first piston (\( A_1 \)) with its unit.
Enter the area of the second piston (\( A_2 \)) with its unit.
Enter the force on the second piston (\( F_2 \)) with its unit.
Convert \( A_1 \), \( A_2 \), and \( F_2 \) to SI units (m², m², N).
Calculate the force on the first piston: \( F_1 = \frac{A_1}{A_2} F_2 \).
Calculate the pressure: \( p = \frac{F_2}{A_2} \).
Convert results to the selected output units and display them, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 5 decimal places.

3. Importance of Pascal's Law Calculation

Calculating forces and pressure using Pascal's law is crucial for:

System Design: Designing hydraulic systems like lifts, presses, and jacks to achieve force multiplication.
Safety: Ensuring the system can handle the pressure without failure.
Efficiency: Optimizing piston areas to achieve the desired force ratio.

4. Using the Calculator

Example 1 (SI Units): Calculate the forces and pressure in a hydraulic system:

Area of First Piston: \( A_1 = 0.000707 \, \text{m}^2 \);
Area of Second Piston: \( A_2 = 0.070686 \, \text{m}^2 \);
Force on Second Piston: \( F_2 = 9806.65 \, \text{N} \);
Force on First Piston: \( F_1 = \frac{0.000707}{0.070686} \times 9806.65 \approx 98.07 \, \text{N} \);
Pressure: \( p = \frac{9806.65}{0.070686} \approx 138730.5 \, \text{Pa} \);
Convert \( p \) to kPa: \( p = 138730.5 / 1000 \approx 138.7305 \, \text{kPa} \);
Result: \( F_1 = 98.07000 \, \text{N} \), \( F_2 = 9806.65000 \, \text{N} \), \( p = 138.73050 \, \text{kPa} \).

Example 2 (Mixed Units): Calculate the forces and pressure in a hydraulic system:

Area of First Piston: \( A_1 = 3.14 \, \text{in}^2 \);
Convert \( A_1 \): \( A_1 = 3.14 \times 0.00064516 = 0.002026 \, \text{m}^2 \);
Area of Second Piston: \( A_2 = 113.1 \, \text{in}^2 \);
Convert \( A_2 \): \( A_2 = 113.1 \times 0.00064516 = 0.072968 \, \text{m}^2 \);
Force on Second Piston: \( F_2 = 5000 \, \text{lbf} \);
Convert \( F_2 \): \( F_2 = 5000 \times 4.44822 = 22241.1 \, \text{N} \);
Force on First Piston: \( F_1 = \frac{0.002026}{0.072968} \times 22241.1 \approx 617.5 \, \text{N} \);
Convert \( F_1 \) to lbf: \( F_1 = 617.5 \times 0.224809 \approx 138.8 \, \text{lbf} \);
Convert \( F_2 \) to lbf: \( F_2 = 5000 \, \text{lbf} \);
Pressure: \( p = \frac{22241.1}{0.072968} \approx 304750.5 \, \text{Pa} \);
Convert \( p \) to psi: \( p = 304750.5 \times 0.000145038 \approx 44.2 \, \text{psi} \);
Result: \( F_1 = 138.80000 \, \text{lbf} \), \( F_2 = 5000.00000 \, \text{lbf} \), \( p = 44.20000 \, \text{psi} \).

5. Frequently Asked Questions (FAQ)

Q: What is Pascal's law?
A: Pascal's law states that pressure applied to a confined fluid is transmitted equally in all directions, allowing a small force on a small piston to produce a larger force on a larger piston.

Q: Why does the pressure remain the same in both pistons?
A: In a hydraulic system, the pressure is constant throughout the fluid (assuming no losses). The force varies due to the difference in piston areas: \( F = p A \).

Q: How can I calculate the piston areas if I only have the diameters?
A: For circular pistons, the area is \( A = \pi \left(\frac{d}{2}\right)^2 \). You can calculate the areas separately and input them into this calculator.