Parallel Inductors Calculator

Inductor 1 (\( L_1 \)):

Inductor 2 (\( L_2 \)):

1. What is Parallel Inductors Calculator?

Definition: This calculator computes the equivalent inductance (\( L \)) of multiple inductors connected in parallel.

Purpose: It is used in electrical engineering to determine the total inductance of a parallel combination of inductors, which is essential for designing circuits such as filters, oscillators, and power supplies.

2. How Does the Calculator Work?

The calculator uses the following formula:

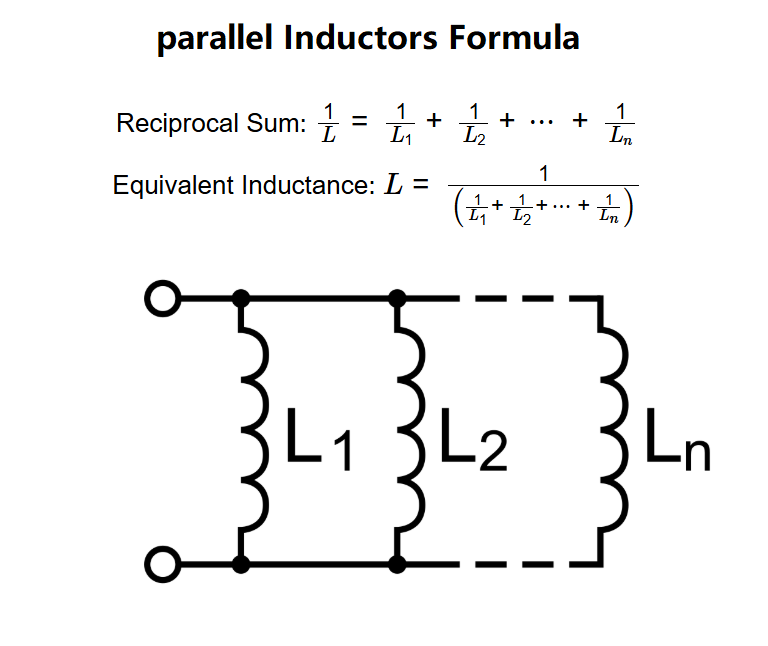
Reciprocal Sum: \( \frac{1}{L} = \frac{1}{L_1} + \frac{1}{L_2} + \cdots + \frac{1}{L_n} \)
Equivalent Inductance: \( L = \frac{1}{\left( \frac{1}{L_1} + \frac{1}{L_2} + \cdots + \frac{1}{L_n} \right)} \)

Where:

\( L \): Equivalent inductance (H)
\( L_1, L_2, \ldots, L_n \): Inductances of the individual inductors (H)

Steps:

Enter the inductance values of the inductors (\( L_1, L_2, \ldots, L_n \)) with their units.
Add or remove inductor fields as needed (minimum of 2 inductors).
Convert all inputs to base units (H).
Calculate the equivalent inductance using the formula.
Convert the result to the selected output unit (H, mH, µH).
Display the result: if the value is less than 0.001 in the selected unit, use scientific notation; otherwise, display with 4 decimal places.

3. Importance of Parallel Inductors Calculation

Calculating the equivalent inductance of inductors in parallel is crucial for:

Circuit Design: Determining the total inductance in a circuit with parallel inductors, which affects the circuit's behavior in applications like filters and resonant circuits.
Energy Storage: Understanding the combined inductance helps in calculating the total energy stored in the magnetic field of the inductors.
Impedance Matching: Adjusting the inductance in a circuit to match the impedance for optimal performance in RF and audio applications.

4. Using the Calculator

Example 1: Calculate the equivalent inductance of two inductors in parallel with \( L_1 = 10 \, \text{mH} \) and \( L_2 = 20 \, \text{mH} \):

Inductor 1 (\( L_1 \)): 10 mH = \( 10 \times 10^{-3} \) H
Inductor 2 (\( L_2 \)): 20 mH = \( 20 \times 10^{-3} \) H
Reciprocal Sum: \( \frac{1}{L} = \frac{1}{10 \times 10^{-3}} + \frac{1}{20 \times 10^{-3}} = 100 + 50 = 150 \)
Equivalent Inductance (\( L \)): \( L = \frac{1}{150} \approx 0.006667 \, \text{H} \), in mH: \( 0.006667 \times 1000 = 6.667 \, \text{mH} \)
Result: \( L = 6.6667 \, \text{mH} \)

Example 2 (Demonstrating Scientific Notation): Calculate the equivalent inductance of three inductors in parallel with \( L_1 = 1 \, \text{µH} \), \( L_2 = 2 \, \text{µH} \), and \( L_3 = 4 \, \text{µH} \):

Inductor 1 (\( L_1 \)): 1 µH = \( 1 \times 10^{-6} \) H
Inductor 2 (\( L_2 \)): 2 µH = \( 2 \times 10^{-6} \) H
Inductor 3 (\( L_3 \)): 4 µH = \( 4 \times 10^{-6} \) H
Reciprocal Sum: \( \frac{1}{L} = \frac{1}{1 \times 10^{-6}} + \frac{1}{2 \times 10^{-6}} + \frac{1}{4 \times 10^{-6}} = 1 \times 10^6 + 0.5 \times 10^6 + 0.25 \times 10^6 = 1.75 \times 10^6 \)
Equivalent Inductance (\( L \)): \( L = \frac{1}{1.75 \times 10^6} \approx 5.714 \times 10^{-7} \, \text{H} \), in µH: \( 5.714 \times 10^{-7} \times 10^6 = 0.5714 \, \text{µH} \)
Result: \( L = 0.5714 \, \text{µH} \)

5. Frequently Asked Questions (FAQ)

Q: What is the equivalent inductance of inductors in parallel?
A: The equivalent inductance of inductors in parallel is calculated using the reciprocal formula: \( \frac{1}{L} = \frac{1}{L_1} + \frac{1}{L_2} + \cdots + \frac{1}{L_n} \). This means the total inductance is always less than the smallest individual inductance.

Q: Why is the equivalent inductance smaller than the individual inductances?
A: In a parallel configuration, the total inductance decreases because the current is divided among the inductors, reducing the effective opposition to current change. The reciprocal formula reflects this behavior.

Q: Can I use this calculator for inductors with different units?
A: Yes, the calculator allows you to specify the unit (H, mH, µH) for each inductor. It converts all values to henries (H) for calculation and then converts the result to the selected output unit.