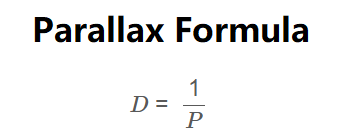1. What is Parallax Calculator?
Definition: This calculator computes the distance (\( D \)) to a star based on its parallax angle (\( P \)), using the parallax method.
Purpose: It is used in astronomy to measure distances to nearby stars by observing their apparent shift in position (parallax) when viewed from two different positions, typically separated by the Earth's orbit (2 AU).
2. How Does the Calculator Work?
The calculator uses the following formula:
Formula:
\[
D = \frac{1}{P}
\]
Where:
- \( D \): Distance to the star (pc, MLy, Mpc)
- \( P \): Parallax angle (arcsec, marcsec, μarcsec)
Unit Conversions:
- Parallax Angle (\( P \)):
- 1 arcsec = 1 arcsec
- 1 marcsec = 0.001 arcsec
- 1 μarcsec = 0.000001 arcsec
- Distance (\( D \)):
- 1 pc = 1 parsec
- 1 MLy = 3.262 light years = \( 3.262 \times 10^6 \) pc
- 1 Mpc = 1,000,000 pc
Steps:
- Select a star from the list or choose "Custom" to input your own parallax angle.
- If "Custom" is selected, enter the parallax angle (\( P \)) with its respective unit (arcsec, marcsec, μarcsec).
- Select the desired unit for the distance result (pc, MLy, Mpc).
- Convert the parallax angle to arcseconds.
- Calculate the distance using \( D = \frac{1}{P} \) in parsecs.
- Convert the distance to the selected unit.
- Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.
3. Importance of Parallax Calculation
Calculating the distance to a star using parallax is crucial for:
- Distance Measurement: Parallax is one of the most direct methods to measure distances to nearby stars, forming the basis of the cosmic distance ladder.
- Stellar Properties: Knowing a star's distance allows astronomers to calculate its intrinsic brightness (absolute magnitude) and other properties.
- Galactic Mapping: Parallax measurements help map the structure of our galaxy by providing accurate distances to stars.
4. Using the Calculator
Examples:
- Example 1: Calculate the distance to Sirius (\( P = 379.2 \, \text{marcsec} \)), with the result in parsecs:
- Select Sirius (α Canis Majoris).
- Parallax: \( P = 379.2 \) marcsec.
- Convert to arcseconds: \( P = 379.2 / 1000 = 0.3792 \) arcsec.
- \( D = \frac{1}{0.3792} \approx 2.6371 \) pc
- Result: \( D = 2.6371 \) pc
- Example 2: Calculate the distance to a star with a custom parallax of 100 marcsec, with the result in mega light years:
- Select "Custom".
- Enter \( P = 100 \) marcsec.
- Convert to arcseconds: \( P = 100 / 1000 = 0.1 \) arcsec.
- \( D = \frac{1}{0.1} = 10 \) pc
- Convert to MLy: \( D = 10 \times 3.262 \times 10^{-6} = 3.262 \times 10^{-5} \) MLy
- Result: \( D = 3.2620e-5 \) MLy
5. Frequently Asked Questions (FAQ)
Q: What is stellar parallax?
A: Stellar parallax is the apparent shift in a star's position when observed from two different points, typically separated by the Earth's orbit (2 AU). It is used to measure distances to nearby stars.
Q: What is a parsec?
A: A parsec (pc) is the distance at which a star would have a parallax angle of 1 arcsecond. It is approximately 3.262 light years or 3.08568e16 meters.
Q: Why are parallax angles often small?
A: Parallax angles are small because even nearby stars are extremely far away, so the angular shift is tiny when observed from opposite sides of the Earth's orbit.
 Home
Home
 Back
Back