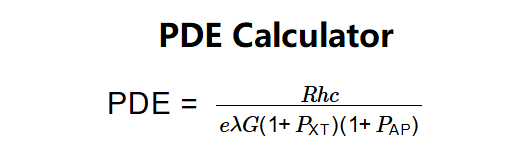PDE Calculator

Photon Detection Efficiency (PDE) Calculator for SiPMs

Responsivity (\( R \)) (A/W):

Wavelength (\( \lambda \)):

Gain (\( G \)):

Crosstalk Probability (\( P_{\text{XT}} \)) (0–1):

Afterpulsing Probability (\( P_{\text{AP}} \)) (0–1):

1. What is Photon Detection Efficiency (PDE) Calculator for SiPMs?

Definition: This calculator computes the Photon Detection Efficiency (PDE) of Silicon Photomultipliers (SiPMs), a measure of their sensitivity to incident photons.

Purpose: It is used in photonics and particle physics to evaluate the performance of SiPMs in applications like medical imaging, LIDAR, and high-energy physics experiments.

2. How Does the Calculator Work?

The calculator uses the formula for PDE in SiPMs:

\( \text{PDE} = \frac{R h c}{e \lambda G (1 + P_{\text{XT}}) (1 + P_{\text{AP}})} \)

Where:

\( \text{PDE} \): Photon Detection Efficiency (%);
\( R \): Responsivity (A/W);
\( h = 6.626 \times 10^{-34} \, \text{m}^2 \text{kg/s} \): Planck’s constant;
\( c = 2.998 \times 10^8 \, \text{m/s} \): Speed of light;
\( e = 1.602 \times 10^{-19} \, \text{C} \): Elementary charge;
\( \lambda \): Wavelength of incident light (m);
\( G \): Gain;
\( P_{\text{XT}} \): Crosstalk probability (0–1);
\( P_{\text{AP}} \): Afterpulsing probability (0–1).

Steps:

Enter the responsivity (\( R \)), wavelength (\( \lambda \)), gain (\( G \)), crosstalk probability (\( P_{\text{XT}} \)), and afterpulsing probability (\( P_{\text{AP}} \)).
Convert wavelength to meters (m).
Calculate the PDE using the formula above.
Convert the result to a percentage.
Display the result with 4 decimal places.

3. Importance of PDE Calculation for SiPMs

Calculating the PDE of SiPMs is crucial for:

Detector Performance: Assessing the efficiency of SiPMs in detecting photons, critical for applications like PET scanners and gamma-ray detectors.
System Optimization: Optimizing SiPM parameters (e.g., gain, crosstalk) to improve overall system performance.
Research Applications: Ensuring accurate photon counting in high-energy physics experiments, such as those in particle accelerators.

4. Using the Calculator

Example 1: Calculate the PDE for an SiPM with \( R = 0.3 \, \text{A/W} \), \( \lambda = 500 \, \text{nm} \), \( G = 1 \times 10^6 \), \( P_{\text{XT}} = 0.2 \), and \( P_{\text{AP}} = 0.1 \):

Input Values:
\( R = 0.3 \, \text{A/W} \);
\( \lambda = 500 \, \text{nm} = 500 \times 10^{-9} = 5 \times 10^{-7} \, \text{m} \);
\( G = 1 \times 10^6 \);
\( P_{\text{XT}} = 0.2 \);
\( P_{\text{AP}} = 0.1 \);
\( h = 6.626 \times 10^{-34} \, \text{m}^2 \text{kg/s} \);
\( c = 2.998 \times 10^8 \, \text{m/s} \);
\( e = 1.602 \times 10^{-19} \, \text{C} \).
Numerator: \( R h c = 0.3 \times 6.626 \times 10^{-34} \times 2.998 \times 10^8 \approx 5.961 \times 10^{-26} \);
Denominator: \( e \lambda G (1 + P_{\text{XT}}) (1 + P_{\text{AP}}) = 1.602 \times 10^{-19} \times 5 \times 10^{-7} \times 1 \times 10^6 \times (1 + 0.2) \times (1 + 0.1) \);
\( = 1.602 \times 10^{-19} \times 5 \times 10^{-7} \times 1 \times 10^6 \times 1.2 \times 1.1 \approx 1.058 \times 10^{-19} \);
PDE: \( \frac{5.961 \times 10^{-26}}{1.058 \times 10^{-19}} \times 100 \approx 0.05634 \times 100 = 5.634\% \);
Result: \( \text{PDE} = 5.6340\% \).

Example 2: Calculate the PDE for an SiPM with \( R = 0.5 \, \text{A/W} \), \( \lambda = 600 \, \text{nm} \), \( G = 5 \times 10^5 \), \( P_{\text{XT}} = 0.15 \), and \( P_{\text{AP}} = 0.05 \):

Input Values:
\( R = 0.5 \, \text{A/W} \);
\( \lambda = 600 \, \text{nm} = 600 \times 10^{-9} = 6 \times 10^{-7} \, \text{m} \);
\( G = 5 \times 10^5 \);
\( P_{\text{XT}} = 0.15 \);
\( P_{\text{AP}} = 0.05 \);
\( h = 6.626 \times 10^{-34} \, \text{m}^2 \text{kg/s} \);
\( c = 2.998 \times 10^8 \, \text{m/s} \);
\( e = 1.602 \times 10^{-19} \, \text{C} \).
Numerator: \( R h c = 0.5 \times 6.626 \times 10^{-34} \times 2.998 \times 10^8 \approx 9.935 \times 10^{-26} \);
Denominator: \( e \lambda G (1 + P_{\text{XT}}) (1 + P_{\text{AP}}) = 1.602 \times 10^{-19} \times 6 \times 10^{-7} \times 5 \times 10^5 \times (1 + 0.15) \times (1 + 0.05) \);
\( = 1.602 \times 10^{-19} \times 6 \times 10^{-7} \times 5 \times 10^5 \times 1.15 \times 1.05 \approx 5.806 \times 10^{-20} \);
PDE: \( \frac{9.935 \times 10^{-26}}{5.806 \times 10^{-20}} \times 100 \approx 0.1711 \times 100 = 17.11\% \);
Result: \( \text{PDE} = 17.1100\% \).

5. Frequently Asked Questions (FAQ)

Q: What factors affect the PDE of an SiPM?
A: The PDE is influenced by the responsivity (\( R \)), wavelength (\( \lambda \)), gain (\( G \)), crosstalk (\( P_{\text{XT}} \)), and afterpulsing (\( P_{\text{AP}} \)). Higher responsivity and lower crosstalk/afterpulsing probabilities increase the PDE.

Q: Why does wavelength affect the PDE?
A: The energy of a photon (\( E = \frac{h c}{\lambda} \)) depends on its wavelength. Shorter wavelengths (higher energy) may interact differently with the SiPM’s material, affecting detection efficiency.

Q: How can I improve the PDE of an SiPM?
A: To improve PDE, you can increase the responsivity by optimizing the sensor design, reduce crosstalk and afterpulsing through better manufacturing, or operate at a wavelength where the SiPM is most sensitive.