Orifice Flow Calculator

Orifice Diameter (\( d \)):

Coefficient of Discharge (\( C_d \)):

Mean Center Line Height (\( H \)):

Acceleration due to Gravity (\( g \)):

1. What is Orifice Flow Calculator?

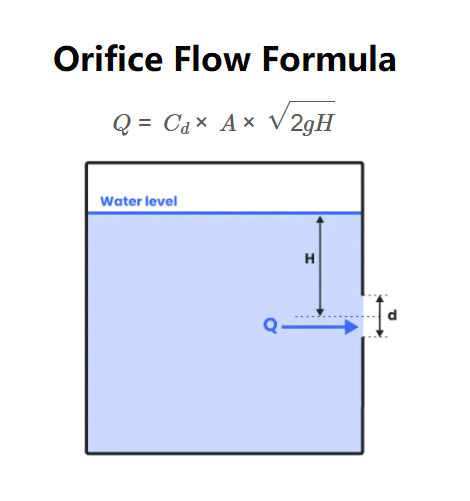
Definition: This calculator computes the flow rate (\( Q \)) through an orifice, based on the orifice diameter (\( d \)), coefficient of discharge (\( C_d \)), mean center line height (\( H \)), and acceleration due to gravity (\( g \)).

Purpose: It is used in fluid mechanics and engineering to determine the volumetric flow rate of a liquid or gas through an orifice, which is common in applications like flow measurement, irrigation systems, and industrial processes.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula: \[ Q = C_d \times A \times \sqrt{2 g H} \] Where:

\( Q \): Flow rate (m³/s, L/s, m³/min, ft³/s, ft³/min)
\( C_d \): Coefficient of discharge (dimensionless, typically between 0 and 1)
\( A \): Area of the orifice (m²), calculated as \( A = \frac{\pi d^2}{4} \)
\( d \): Diameter of the orifice (m, cm, mm, ft, in)
\( g \): Acceleration due to gravity (m/s², ft/s²)
\( H \): Mean center line height (m, cm, mm, ft, in)

Unit Conversions:

Diameter (\( d \)) and Height (\( H \)):
- 1 m = 1 m
- 1 cm = 0.01 m
- 1 mm = 0.001 m
- 1 ft = 0.3048 m
- 1 in = 0.0254 m
Acceleration due to Gravity (\( g \)):
- 1 m/s² = 1 m/s²
- 1 ft/s² = 0.3048 m/s²
Flow Rate (\( Q \)):
- 1 m³/s = 1 m³/s
- 1 L/s = 0.001 m³/s
- 1 m³/min = \( \frac{1}{60} \) m³/s
- 1 ft³/s = \( (0.3048)^3 \) m³/s
- 1 ft³/min = \( \frac{(0.3048)^3}{60} \) m³/s

Steps:

Enter the orifice diameter (\( d \)) with its respective unit (m, cm, mm, ft, in).
Enter the coefficient of discharge (\( C_d \)).
Enter the mean center line height (\( H \)) with its respective unit (m, cm, mm, ft, in).
Enter the acceleration due to gravity (\( g \)) with its respective unit (m/s², ft/s²). Default is 9.81 m/s² (Earth's gravity).
Convert all inputs to SI units (m for diameter and height, m/s² for gravity).
Calculate the area of the orifice using \( A = \frac{\pi d^2}{4} \).
Calculate the flow rate using \( Q = C_d \times A \times \sqrt{2 g H} \).
Display the result in the selected unit (m³/s, L/s, m³/min, ft³/s, ft³/min), using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Orifice Flow Calculation

Calculating the orifice flow rate is crucial for:

Flow Measurement: Determining the flow rate of fluids in pipes, tanks, and other systems using orifice plates.
Engineering Design: Designing irrigation systems, HVAC systems, and industrial processes where precise flow control is needed.
Fluid Dynamics Research: Studying the behavior of fluids through constrictions in experimental setups.

4. Using the Calculator

Examples:

Example 1: Calculate the flow rate through an orifice with a diameter of 50 mm, coefficient of discharge 0.8, mean center line height of 200 mm, and acceleration due to gravity 9.81 m/s², with flow rate in m³/s:
- Enter \( d = 50 \) mm.
- Convert to m: \( d = 50 \times 0.001 = 0.05 \, \text{m} \)
- Enter \( C_d = 0.8 \).
- Enter \( H = 200 \) mm.
- Convert to m: \( H = 200 \times 0.001 = 0.2 \, \text{m} \)
- Enter \( g = 9.81 \) m/s².
- Area: \( A = \frac{\pi (0.05)^2}{4} = 0.0019635 \, \text{m²} \)
- Flow rate: \( Q = 0.8 \times 0.0019635 \times \sqrt{2 \times 9.81 \times 0.2} = 0.0311 \, \text{m³/s} \)
- Result: \( Q = 0.0311 \, \text{m³/s} \)
Example 2: Calculate the flow rate through an orifice with a diameter of 2 in, coefficient of discharge 0.6, mean center line height of 1 ft, and acceleration due to gravity 32.174 ft/s², with flow rate in ft³/s:
- Enter \( d = 2 \) in.
- Convert to m: \( d = 2 \times 0.0254 = 0.0508 \, \text{m} \)
- Enter \( C_d = 0.6 \).
- Enter \( H = 1 \) ft.
- Convert to m: \( H = 1 \times 0.3048 = 0.3048 \, \text{m} \)
- Enter \( g = 32.174 \) ft/s².
- Convert to m/s²: \( g = 32.174 \times 0.3048 = 9.8066 \, \text{m/s²} \)
- Area: \( A = \frac{\pi (0.0508)^2}{4} = 0.002027 \, \text{m²} \)
- Flow rate: \( Q = 0.6 \times 0.002027 \times \sqrt{2 \times 9.8066 \times 0.3048} = 0.0298 \, \text{m³/s} \)
- Convert to ft³/s: \( Q = 0.0298 / (0.3048)^3 = 1.0525 \, \text{ft³/s} \)
- Result: \( Q = 1.0525 \, \text{ft³/s} \)

5. Frequently Asked Questions (FAQ)

Q: What is the coefficient of discharge (\( C_d \))?
A: The coefficient of discharge (\( C_d \)) accounts for losses due to friction, contraction, and other effects in the orifice, typically ranging from 0 to 1. A value of 0.8 is common for well-designed orifices.

Q: Why must the mean center line height be positive?
A: The mean center line height (\( H \)) represents the head of fluid driving the flow through the orifice. It must be positive for the flow to occur.

Q: Can this calculator be used for gases?
A: This calculator is primarily designed for incompressible fluids (liquids). For gases, compressibility effects may need to be considered, requiring a different approach.