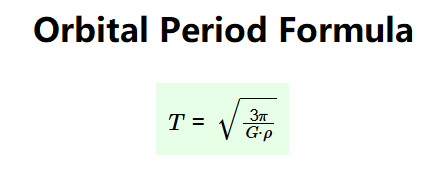Orbital Period Calculator

1. What is Orbital Period Calculator?

Definition: This calculator computes the orbital period (\( T \)) of a small satellite in a low orbit around a central body using a simplified form of the orbital period equation, based on the mean density of the central body (\( \rho \)) and the universal gravitational constant (\( G \)).

Purpose: It is used in astronomy and aerospace engineering to determine the time it takes for a satellite to complete one orbit around a central body, such as a satellite in low Earth orbit.

2. How Does the Calculator Work?

The calculator uses a simplified orbital period equation for a satellite in a low orbit:

\( T = \sqrt{\frac{3 \pi}{G \cdot \rho}} \)

Where:

\( T \): Orbital period (s)
\( G \): Universal gravitational constant (\( G = 6.67430 \times 10^{-11} \, \text{m}^3 \text{kg}^{-1} \text{s}^{-2} \))
\( \rho \): Mean density of the central body (kg/m³)

Unit Conversions:

Mean Density (\( \rho \)):
- 1 kg/m³ = 1 kg/m³
- 1 g/cm³ = 1000 kg/m³
- 1 lb/cu ft = 16.0185 kg/m³
- 1 lb/cu yd = 0.593276 kg/m³
- 1 kg/cm³ = 1,000,000 kg/m³
- 1 mg/cm³ = 1 kg/m³
- 1 g/m³ = 0.001 kg/m³
Orbital Period (\( T \)):
- 1 second = 1 s
- 1 minute = 60 s
- 1 hour = 3600 s
- 1 day = 86400 s
- 1 week = 604800 s
- 1 month = 2629800 s (approximate, using 30.417 days)
- 1 year = 31557600 s (accounting for leap years, 365.25 days)

Steps:

Enter the mean density of the central body (\( \rho \)) with its respective unit.
Convert the density to base units (kg/m³).
Calculate \( T \) using the simplified orbital period equation.
Convert the result to the selected unit for display (seconds, minutes, hours, days, weeks, months, or years).
Display the result with 4 decimal places.

3. Importance of Orbital Period Calculation

Calculating the orbital period is crucial for:

Satellite Operations: Determining how often a satellite passes over a specific point on Earth, which is essential for communication, weather monitoring, and navigation satellites.
Space Mission Planning: Understanding the timing of orbits for rendezvous, docking, or observational missions.
Astronomical Studies: Estimating the orbital behavior of satellites or other objects around planets or stars.

4. Using the Calculator

Example: Calculate the orbital period of a satellite in low Earth orbit around Earth, given Earth’s mean density \( \rho = 5514 \, \text{kg/m}^3 \).

Enter \( \rho = 5514 \, \text{kg/m}^3 \).
The calculator computes:
- \( T = \sqrt{\frac{3 \pi}{G \cdot \rho}} = \sqrt{\frac{3 \pi}{(6.67430 \times 10^{-11}) \cdot 5514}} \approx \sqrt{\frac{9.4248}{3.681 \times 10^{-7}}} \approx \sqrt{2.561 \times 10^7} \approx 5060.7 \, \text{seconds} \).
- In minutes: \( 5060.7 / 60 \approx 84.345 \, \text{minutes} \), which is roughly 84 minutes, a typical period for a low Earth orbit.

5. Frequently Asked Questions (FAQ)

Q: What is the orbital period?
A: The orbital period (\( T \)) is the time it takes for a satellite to complete one full orbit around a central body, such as Earth.

Q: What is the simplified orbital period equation?
A: For a satellite in a low orbit, the orbital period can be approximated as \( T = \sqrt{\frac{3 \pi}{G \cdot \rho}} \), where \( G \) is the gravitational constant and \( \rho \) is the mean density of the central body.

Q: How does the calculator handle different units?
A: The calculator allows users to input density in kg/m³, g/cm³, lb/cu ft, lb/cu yd, kg/cm³, mg/cm³, or g/m³, and converts all inputs to kg/m³ for calculation. The result can be displayed in seconds, minutes, hours, days, weeks, months, or years, based on user selection.