Oblique Shock Calculator

Turn Angle (\( \theta \)):

Downstream Mach Number (\( M_2 \)):

Pressure Ratio (\( \frac{p_2}{p_1} \)):

Density Ratio (\( \frac{\rho_2}{\rho_1} \)):

Temperature Ratio (\( \frac{T_2}{T_1} \)):

Stagnation Pressure Ratio (\( \frac{p_{02}}{p_{01}} \)):

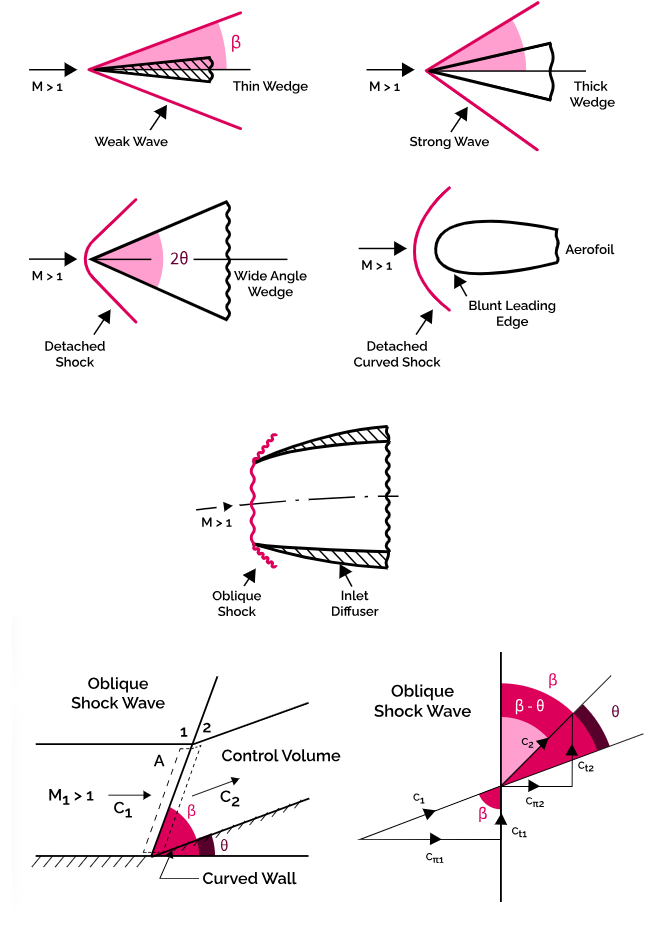
1. What is Oblique Shock Calculator?

Definition: This calculator computes the properties of an oblique shock wave, including the turn angle (\( \theta \)), downstream Mach number (\( M_2 \)), pressure ratio (\( \frac{p_2}{p_1} \)), density ratio (\( \frac{\rho_2}{\rho_1} \)), temperature ratio (\( \frac{T_2}{T_1} \)), and stagnation pressure ratio (\( \frac{p_{02}}{p_{01}} \)), based on the upstream Mach number (\( M_1 \)), wave angle (\( \beta \)), and specific heat ratio (\( \gamma \)).

Purpose: It is used in aerodynamics to analyze the behavior of shock waves in supersonic flows, such as those encountered in high-speed aircraft, missiles, and spacecraft.

2. How Does the Calculator Work?

The calculator uses the following formulas:

Formulas: \[ \tan \theta = \frac{2 \cot \beta (M_1^2 \sin^2 \beta - 1)}{M_1^2 (\gamma + \cos 2\beta) + 2} \] \[ M_{1n} = M_1 \sin \beta \] \[ M_{2n}^2 = \frac{1 + \frac{\gamma - 1}{2} M_{1n}^2}{\gamma M_{1n}^2 - \frac{\gamma - 1}{2}} \] \[ M_2 = \frac{M_{2n}}{\sin (\beta - \theta)} \] \[ \frac{p_2}{p_1} = 1 + \frac{2 \gamma}{\gamma + 1} (M_{1n}^2 - 1) \] \[ \frac{\rho_2}{\rho_1} = \frac{(\gamma + 1) M_{1n}^2}{2 + (\gamma - 1) M_{1n}^2} \] \[ \frac{T_2}{T_1} = \frac{[2 \gamma M_{1n}^2 - (\gamma - 1)][2 + (\gamma - 1) M_{1n}^2]}{(\gamma + 1)^2 M_{1n}^2} \] \[ \frac{p_{02}}{p_{01}} = \left[ \frac{(\gamma + 1) M_{1n}^2}{2 + (\gamma - 1) M_{1n}^2} \right]^{\frac{\gamma}{\gamma - 1}} \times \left[ \frac{\gamma + 1}{2 \gamma M_{1n}^2 - (\gamma - 1)} \right]^{\frac{1}{\gamma - 1}} \] Where:

\( M_1 \): Upstream Mach number
\( M_2 \): Downstream Mach number
\( M_{1n} \): Normal component of upstream Mach number
\( M_{2n} \): Normal component of downstream Mach number
\( \beta \): Wave angle (degrees or radians)
\( \theta \): Turn angle (degrees or radians)
\( \gamma \): Specific heat ratio (typically 1.4 for air)
\( p_2/p_1 \): Pressure ratio across the shock
\( \rho_2/\rho_1 \): Density ratio across the shock
\( T_2/T_1 \): Temperature ratio across the shock
\( p_{02}/p_{01} \): Stagnation pressure ratio across the shock

Unit Conversions:

Wave Angle (\( \beta \)) and Turn Angle (\( \theta \)):
- 1 degree = \( \pi / 180 \) radians
- 1 radian = \( 180 / \pi \) degrees

Steps:

Enter the upstream Mach number (\( M_1 \)).
Enter the wave angle (\( \beta \)) with its respective unit (degrees or radians).
Enter the specific heat ratio (\( \gamma \)). Default is 1.4 (typical for air).
Convert the wave angle to radians for calculation.
Calculate the turn angle (\( \theta \)) using the \(\theta-\beta-M\) relation.
Calculate the normal component of the upstream Mach number (\( M_{1n} \)).
Calculate the normal component of the downstream Mach number (\( M_{2n} \)).
Calculate the downstream Mach number (\( M_2 \)) using the oblique shock geometry.
Calculate the pressure ratio (\( \frac{p_2}{p_1} \)), density ratio (\( \frac{\rho_2}{\rho_1} \)), temperature ratio (\( \frac{T_2}{T_1} \)), and stagnation pressure ratio (\( \frac{p_{02}}{p_{01}} \)) using the respective formulas.
Display the results, using scientific notation for values less than 0.001, otherwise with 4 decimal places.
Select the desired unit for the turn angle (\( \theta \)) from the dropdown to convert the result.

3. Importance of Oblique Shock Calculation

Calculating oblique shock properties is crucial for:

Aerospace Design: Designing supersonic aircraft and spacecraft to manage shock waves, which affect drag, lift, and structural integrity.
Performance Analysis: Understanding changes in pressure, density, and temperature across a shock to optimize engine inlets and nozzles.
Research: Studying high-speed aerodynamics in wind tunnels and computational fluid dynamics simulations.

4. Using the Calculator

Examples:

Example 1: Calculate the oblique shock properties for an upstream Mach number \( M_1 = 5 \), wave angle \( \beta = 20^\circ \), and specific heat ratio \( \gamma = 1.4 \), with turn angle in degrees:
- Enter \( M_1 = 5 \).
- Enter \( \beta = 20 \) degrees.
- Convert to radians: \( \beta = 20 \times \pi / 180 = 0.3491 \, \text{rad} \)
- Enter \( \gamma = 1.4 \).
- \( \sin \beta = \sin(0.3491) = 0.3420 \), \( \cot \beta = 1 / \tan(0.3491) = 2.7475 \), \( \cos 2\beta = \cos(2 \times 0.3491) = 0.7660 \)
- \( M_{1n} = 5 \times 0.3420 = 1.7101 \), \( M_{1n}^2 = 2.9245 \)
- Turn angle: \( \tan \theta = \frac{2 \times 2.7475 \times (2.9245 - 1)}{5^2 \times (1.4 + 0.7660) + 2} = 0.1864 \)
- \( \theta = \arctan(0.1864) = 0.1845 \, \text{rad} = 0.1845 \times 180 / \pi = 10.5667^\circ \)
- Downstream normal Mach number: \( M_{2n}^2 = \frac{1 + \frac{1.4 - 1}{2} \times 2.9245}{1.4 \times 2.9245 - \frac{1.4 - 1}{2}} = 0.5575 \), \( M_{2n} = 0.7467 \)
- Downstream Mach number: \( M_2 = \frac{0.7467}{\sin(0.3491 - 0.1845)} = 2.1595 \)
- Pressure ratio: \( \frac{p_2}{p_1} = 1 + \frac{2 \times 1.4}{1.4 + 1} (2.9245 - 1) = 3.2455 \)
- Density ratio: \( \frac{\rho_2}{\rho_1} = \frac{(1.4 + 1) \times 2.9245}{2 + (1.4 - 1) \times 2.9245} = 2.2144 \)
- Temperature ratio: \( \frac{T_2}{T_1} = \frac{[2 \times 1.4 \times 2.9245 - (1.4 - 1)][2 + (1.4 - 1) \times 2.9245]}{(1.4 + 1)^2 \times 2.9245} = 1.4655 \)
- Stagnation pressure ratio: \( \frac{p_{02}}{p_{01}} = \left( \frac{(1.4 + 1) \times 2.9245}{2 + (1.4 - 1) \times 2.9245} \right)^{\frac{1.4}{1.4 - 1}} \times \left( \frac{1.4 + 1}{2 \times 1.4 \times 2.9245 - (1.4 - 1)} \right)^{\frac{1}{1.4 - 1}} = 0.4545 \)
- Result: \( \theta = 10.5667^\circ \), \( M_2 = 2.1595 \), \( \frac{p_2}{p_1} = 3.2455 \), \( \frac{\rho_2}{\rho_1} = 2.2144 \), \( \frac{T_2}{T_1} = 1.4655 \), \( \frac{p_{02}}{p_{01}} = 0.4545 \)
Example 2: Calculate the oblique shock properties for an upstream Mach number \( M_1 = 3 \), wave angle \( \beta = 0.5236 \, \text{rad} \) (30°), and specific heat ratio \( \gamma = 1.4 \), with turn angle in radians:
- Enter \( M_1 = 3 \).
- Enter \( \beta = 0.5236 \) rad (equivalent to 30°).
- Enter \( \gamma = 1.4 \).
- \( \sin \beta = \sin(0.5236) = 0.5 \), \( \cot \beta = 1 / \tan(0.5236) = 1.7321 \), \( \cos 2\beta = \cos(2 \times 0.5236) = 0.5 \)
- \( M_{1n} = 3 \times 0.5 = 1.5 \), \( M_{1n}^2 = 2.25 \)
- Turn angle: \( \tan \theta = \frac{2 \times 1.7321 \times (2.25 - 1)}{3^2 \times (1.4 + 0.5) + 2} = 0.2357 \)
- \( \theta = \arctan(0.2357) = 0.2327 \, \text{rad} \)
- Downstream normal Mach number: \( M_{2n}^2 = \frac{1 + \frac{1.4 - 1}{2} \times 2.25}{1.4 \times 2.25 - \frac{1.4 - 1}{2}} = 0.6429 \), \( M_{2n} = 0.8018 \)
- Downstream Mach number: \( M_2 = \frac{0.8018}{\sin(0.5236 - 0.2327)} = 1.8347 \)
- Pressure ratio: \( \frac{p_2}{p_1} = 1 + \frac{2 \times 1.4}{1.4 + 1} (2.25 - 1) = 1.4583 \)
- Density ratio: \( \frac{\rho_2}{\rho_1} = \frac{(1.4 + 1) \times 2.25}{2 + (1.4 - 1) \times 2.25} = 1.2857 \)
- Temperature ratio: \( \frac{T_2}{T_1} = \frac{[2 \times 1.4 \times 2.25 - (1.4 - 1)][2 + (1.4 - 1) \times 2.25]}{(1.4 + 1)^2 \times 2.25} = 1.1343 \)
- Stagnation pressure ratio: \( \frac{p_{02}}{p_{01}} = \left( \frac{(1.4 + 1) \times 2.25}{2 + (1.4 - 1) \times 2.25} \right)^{\frac{1.4}{1.4 - 1}} \times \left( \frac{1.4 + 1}{2 \times 1.4 \times 2.25 - (1.4 - 1)} \right)^{\frac{1}{1.4 - 1}} = 0.8749 \)
- Result: \( \theta = 0.2327 \, \text{rad} \), \( M_2 = 1.8347 \), \( \frac{p_2}{p_1} = 1.4583 \), \( \frac{\rho_2}{\rho_1} = 1.2857 \), \( \frac{T_2}{T_1} = 1.1343 \), \( \frac{p_{02}}{p_{01}} = 0.8749 \)

5. Frequently Asked Questions (FAQ)

Q: What is an oblique shock wave?
A: An oblique shock wave is a type of shock wave that occurs in supersonic flow when the flow is turned at an angle, causing a change in pressure, density, temperature, and Mach number across the shock.

Q: Why must the upstream Mach number be greater than 1?
A: Oblique shock waves only occur in supersonic flows (Mach number greater than 1). For subsonic flows, the flow adjusts smoothly without forming a shock.

Q: What is the significance of the specific heat ratio (\( \gamma \))?
A: The specific heat ratio (\( \gamma \)) represents the ratio of specific heats of the gas (e.g., 1.4 for air) and affects the thermodynamic properties across the shock, such as pressure and temperature changes.