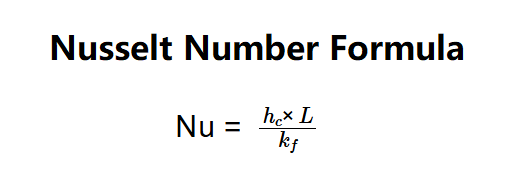Nusselt Number Calculator

Convective Heat Transfer Coefficient (\( h_c \)):

Characteristic Length (\( L \)):

Thermal Conductivity of Fluid (\( k_f \)):

1. What is Nusselt Number Calculator?

Definition: This calculator computes the Nusselt number (\( \text{Nu} \)), a dimensionless quantity that characterizes the convective heat transfer at a solid-fluid interface.

Purpose: It is used in heat transfer analysis to quantify the enhancement of heat transfer due to convection over conduction, aiding in the design of heat exchangers, cooling systems, and thermal management solutions.

2. How Does the Calculator Work?

The calculator uses the Nusselt number formula:

\( \text{Nu} = \frac{h_c \times L}{k_f} \)

Where:

\( h_c \): Convective heat transfer coefficient (W/m²·K);
\( L \): Characteristic length of the solid surface (m);
\( k_f \): Thermal conductivity of the fluid (W/m·K).

Steps:

Enter the convective heat transfer coefficient (\( h_c \)) and its unit (W/m²·K, W/cm²·K, or Btu/h·ft²·°F).
Enter the characteristic length (\( L \)) and its unit (m, cm, mm, or ft).
Enter the thermal conductivity of the fluid (\( k_f \)) and its unit (W/m·K, W/cm·K, or Btu/h·ft·°F).
Convert all inputs to base units (W/m²·K for \( h_c \), m for \( L \), W/m·K for \( k_f \)).
Calculate the Nusselt number using the formula.
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Nusselt Number Calculation

Calculating the Nusselt number is crucial for:

Heat Transfer Analysis: Quantifying the effectiveness of convective heat transfer in systems like heat exchangers and cooling fins.
Engineering Design: Optimizing thermal performance in HVAC systems, electronics cooling, and industrial processes.
Fluid Dynamics: Understanding the relationship between convection and conduction in fluid flow over surfaces.

4. Using the Calculator

Example 1 (Air Flow Over a Surface): Calculate the Nusselt number for air flowing over a surface:

Convective Heat Transfer Coefficient: \( h_c = 25 \, \text{W/m}^2\cdot\text{K} \);
Characteristic Length: \( L = 1 \, \text{m} \);
Thermal Conductivity of Air: \( k_f = 0.026 \, \text{W/m}\cdot\text{K} \);
Nusselt Number: \( \text{Nu} = \frac{25 \times 1}{0.026} \approx 961.5385 \);
Result: \( \text{Nu} = 961.5385 \).

Example 2 (Different Units): Calculate the Nusselt number with different units:

Convective Heat Transfer Coefficient: \( h_c = 4.4 \, \text{Btu/h}\cdot\text{ft}^2\cdot\text{°F} \);
Characteristic Length: \( L = 3 \, \text{ft} \);
Thermal Conductivity of Fluid: \( k_f = 0.015 \, \text{Btu/h}\cdot\text{ft}\cdot\text{°F} \);
Convert units: \( h_c = 4.4 \times 5.678263 = 24.9844 \, \text{W/m}^2\cdot\text{K} \), \( L = 3 \times 0.3048 = 0.9144 \, \text{m} \), \( k_f = 0.015 \times 1.730735 = 0.025961 \, \text{W/m}\cdot\text{K} \);
Nusselt Number: \( \text{Nu} = \frac{24.9844 \times 0.9144}{0.025961} \approx 880.0000 \);
Result: \( \text{Nu} = 880.0000 \).

5. Frequently Asked Questions (FAQ)

Q: What is the Nusselt number?
A: The Nusselt number (\( \text{Nu} \)) is a dimensionless quantity that measures the ratio of convective to conductive heat transfer across a boundary.

Q: What does the characteristic length represent?
A: The characteristic length (\( L \)) is typically the length of the solid surface in the direction of heat transfer, such as the length of a plate or the diameter of a pipe.

Q: Why is the Nusselt number dimensionless?
A: The Nusselt number is dimensionless because it is a ratio of two heat transfer rates (convective and conductive), making it independent of units when computed with consistent units.