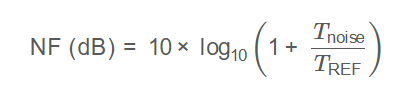1. What is Noise Temperature to Noise Figure Calculator?

Definition: This calculator converts Noise Temperature (in Kelvin) to Noise Figure (in decibels), which measures the degradation of the signal-to-noise ratio caused by a device.

Purpose: It is used in RF engineering and telecommunications to evaluate the noise performance of amplifiers, receivers, and other RF components using a logarithmic scale.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula: $$\text{NF (dB)}=10\times {\log }_{10}(1+\frac{T_{\text{noise}}}{T_{\text{REF}}})$$ Where:

• $\text{NF}$: Noise Figure (dB)
• $T_{\text{noise}}$: Noise Temperature (K)
• $T_{\text{REF}}$: Reference Temperature (K, typically 290 K)

Unit Conversions:

• Noise Temperature ($T_{\text{noise}}$): Measured in Kelvin (K), no conversion needed
• Reference Temperature ($T_{\text{REF}}$): Measured in Kelvin (K), no conversion needed
• Noise Figure (NF): Measured in dB, no conversion needed

Steps:

• Enter the Noise Temperature in Kelvin (non-negative value).
• Enter the Reference Temperature in Kelvin (default is 290 K).
• Calculate $\text{NF (dB)}=10\times {\log }_{10}(1+\frac{T_{\text{noise}}}{T_{\text{REF}}})$.
• Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Noise Temperature to Noise Figure Calculation

Calculating Noise Figure from Noise Temperature is crucial for:

• RF Engineering: Evaluating the noise performance of RF components like low-noise amplifiers (LNAs).
• Telecommunications: Improving the signal-to-noise ratio in receivers for better communication quality.
• System Design: Designing low-noise systems for applications like satellite communications and radar.

4. Using the Calculator

Examples:

• Example 1: For $T_{\text{noise}}=290\text{K}$, $T_{\text{REF}}=290\text{K}$:
  • $\text{NF (dB)}=10\times {\log }_{10}(1+\frac{290}{290})$
  • $\text{NF (dB)}=10\times {\log }_{10}(2)$
  • ${\log }_{10}(2)\approx 0.3010$
  • $\text{NF (dB)}=10\times 0.3010\approx 3.0100\text{dB}$
• Example 2: For $T_{\text{noise}}=0\text{K}$, $T_{\text{REF}}=290\text{K}$:
  • $\text{NF (dB)}=10\times {\log }_{10}(1+\frac{0}{290})$
  • $\text{NF (dB)}=10\times {\log }_{10}(1)$
  • $\text{NF (dB)}=0.0000\text{dB}$

5. Frequently Asked Questions (FAQ)

Q: What is Noise Temperature?
A: Noise Temperature is a measure of the noise power introduced by a system, expressed as an equivalent temperature in Kelvin.

Q: What is Noise Figure?
A: Noise Figure is a logarithmic measure (in dB) of the degradation of the signal-to-noise ratio caused by a device.

Q: How is Noise Temperature to Noise Figure conversion used in real life?
A: It is used in RF system design, such as in satellite communications and radar systems, to evaluate noise performance and optimize signal quality.

Noise Temperature to Noise Figure Calculator© - All Rights Reserved 2025