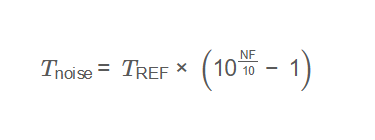Noise Temperature Calculator

1. What is Noise Temperature Calculator?

Definition: This calculator computes the noise temperature (\( T_{\text{noise}} \)) of a system based on the reference temperature (\( T_{\text{REF}} \)) and noise figure (\( \text{NF} \)).

Purpose: It is used in RF engineering and telecommunications to quantify the noise performance of amplifiers, receivers, and other RF components, which is critical for signal-to-noise ratio analysis.

2. How Does the Calculator Work?

The calculator uses the following formula:

Formula: \[ T_{\text{noise}} = T_{\text{REF}} \times \left( 10^{\frac{\text{NF}}{10}} - 1 \right) \] Where:

\( T_{\text{noise}} \): Noise Temperature (K)
\( T_{\text{REF}} \): Reference Temperature (K, typically 290 K)
\( \text{NF} \): Noise Figure (dB)

Unit Conversions:

Reference Temperature (\( T_{\text{REF}} \)): Measured in Kelvin (K), no conversion needed
Noise Figure (\( \text{NF} \)): Measured in decibels (dB), no conversion needed
Noise Temperature (\( T_{\text{noise}} \)): Measured in Kelvin (K), no conversion needed

Steps:

Enter the reference temperature (\( T_{\text{REF}} \)) in Kelvin (default is 290 K).
Enter the noise figure (\( \text{NF} \)) in decibels (dB).
Calculate \( T_{\text{noise}} = T_{\text{REF}} \times \left( 10^{\frac{\text{NF}}{10}} - 1 \right) \).
Display the result, using scientific notation for values less than 0.001, otherwise with 4 decimal places.

3. Importance of Noise Temperature Calculation

Calculating noise temperature is crucial for:

RF Engineering: Evaluating the noise performance of RF components like low-noise amplifiers (LNAs).
Telecommunications: Improving the signal-to-noise ratio in receivers for better communication quality.
Satellite Systems: Designing systems that operate in low-noise environments, such as satellite receivers.

4. Using the Calculator

Examples:

Example 1: For \( T_{\text{REF}} = 290 \, \text{K} \), \( \text{NF} = 3 \, \text{dB} \):
- \( T_{\text{noise}} = 290 \times \left( 10^{\frac{3}{10}} - 1 \right) \)
- \( 10^{\frac{3}{10}} \approx 1.9953 \)
- \( T_{\text{noise}} = 290 \times (1.9953 - 1) \approx 288.6228 \, \text{K} \)
Example 2: For \( T_{\text{REF}} = 290 \, \text{K} \), \( \text{NF} = 0 \, \text{dB} \):
- \( T_{\text{noise}} = 290 \times \left( 10^{\frac{0}{10}} - 1 \right) \)
- \( 10^{\frac{0}{10}} = 1 \)
- \( T_{\text{noise}} = 290 \times (1 - 1) = 0 \, \text{K} \)

5. Frequently Asked Questions (FAQ)

Q: What is noise temperature?
A: Noise temperature (\( T_{\text{noise}} \)) is a measure of the noise power introduced by a system, expressed as an equivalent temperature in Kelvin.

Q: Why is the reference temperature typically 290 K?
A: 290 K (approximately 17°C) is a standard reference temperature used in noise calculations, representing typical ambient conditions.

Q: How is noise temperature used in real life?
A: It is used in designing low-noise systems for applications like radio astronomy, satellite communications, and high-sensitivity receivers.