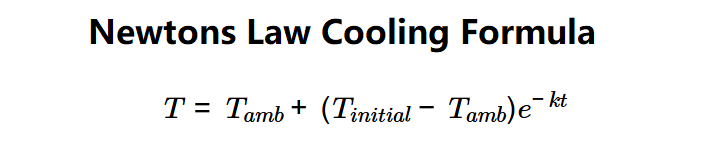Newton's Law of Cooling Calculator

Ambient Temperature (\( T_{amb} \)):

Initial Temperature (\( T_{initial} \)):

Cooling Coefficient (\( k \)):

Cooling Time (\( t \)):

1. What is Newton's Law of Cooling Calculator?

Definition: This calculator computes the temperature of an object after cooling over a period of time, using Newton's Law of Cooling.

Purpose: It is used in physics and engineering to predict how quickly an object cools in a given environment, which is useful for applications like HVAC design, food safety, and material processing.

2. How Does the Calculator Work?

The calculator uses Newton's Law of Cooling formula:

\( T = T_{amb} + (T_{initial} - T_{amb}) e^{-kt} \)

Where:

\( T \): Temperature of the object at time \( t \) (K);
\( T_{amb} \): Ambient temperature (K);
\( T_{initial} \): Initial temperature of the object (K);
\( k \): Cooling coefficient (1/s);
\( t \): Cooling time (s).

Steps:

Enter the ambient temperature (\( T_{amb} \)) and its unit (°C, K, or °F).
Enter the initial temperature of the object (\( T_{initial} \)) and its unit.
Enter the cooling coefficient (\( k \)) in 1/s.
Enter the cooling time (\( t \)) and its unit (s, min, or h).
Convert all temperatures to Kelvin and time to seconds for calculation.
Compute the final temperature \( T \) using the formula.
Convert the final temperature to the selected output unit.
Display the result, formatted in scientific notation if the absolute value is less than 0.001, otherwise with 4 decimal places.

3. Importance of Newton's Law of Cooling Calculation

Calculating the cooling of an object is crucial for:

Thermal Management: Predicting cooling times in HVAC systems, electronics, and industrial processes.
Food Safety: Ensuring food cools to safe temperatures within a specified time to prevent bacterial growth.
Material Science: Analyzing the cooling behavior of materials during manufacturing processes.

4. Using the Calculator

Example 1 (Cooling a Hot Object): Calculate the temperature of an object after cooling:

Ambient Temperature: \( T_{amb} = 25 \, \text{°C} \);
Initial Temperature: \( T_{initial} = 100 \, \text{°C} \);
Cooling Coefficient: \( k = 0.01 \, \text{1/s} \);
Cooling Time: \( t = 300 \, \text{s} \);
Convert to Kelvin: \( T_{amb} = 298.15 \, \text{K} \), \( T_{initial} = 373.15 \, \text{K} \);
Final Temperature: \( T = 298.15 + (373.15 - 298.15) \times e^{-0.01 \times 300} \approx 303.74 \, \text{K} \);
Result in °C: \( T = 303.74 - 273.15 = 30.5869 \, \text{°C} \).

Example 2 (Different Units): Calculate the temperature with different units:

Ambient Temperature: \( T_{amb} = 77 \, \text{°F} \);
Initial Temperature: \( T_{initial} = 373.15 \, \text{K} \);
Cooling Coefficient: \( k = 0.01 \, \text{1/s} \);
Cooling Time: \( t = 5 \, \text{min} \);
Convert units: \( T_{amb} = (77 - 32) \times 5/9 + 273.15 = 298.15 \, \text{K} \), \( T_{initial} = 373.15 \, \text{K} \), \( t = 5 \times 60 = 300 \, \text{s} \);
Final Temperature: \( T \approx 303.74 \, \text{K} \);
Result in °F: \( T = (303.74 - 273.15) \times 9/5 + 32 = 87.0562 \, \text{°F} \).

5. Frequently Asked Questions (FAQ)

Q: What is Newton's Law of Cooling?
A: Newton's Law of Cooling states that the rate of temperature change of an object is proportional to the difference between its temperature and the ambient temperature.

Q: What is the cooling coefficient \( k \)?
A: The cooling coefficient \( k \) (in 1/s) depends on the object's material, surface area, and the surrounding medium, determining how quickly it cools.

Q: What does the Biot number condition mean?
A: The Biot number must be small for Newton's Law to apply, meaning the temperature within the object is roughly uniform, and internal conduction is not a limiting factor.