1. What is the NTC Thermistor Calculator?

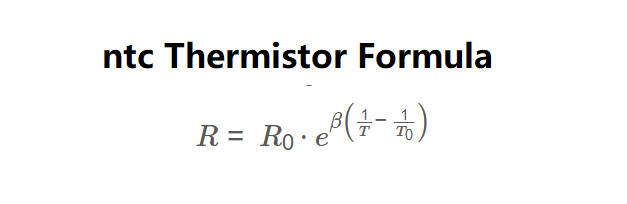
Definition: This calculator determines the resistance of an NTC (Negative Temperature Coefficient) thermistor at a given temperature, using the thermistor's nominal resistance, reference temperature, and beta value. NTC thermistors decrease in resistance as temperature increases.

Purpose: Engineers, technicians, and hobbyists use this tool to design temperature-sensing circuits, calibrate thermistors, or predict thermistor behavior in applications like HVAC systems, medical devices, and automotive electronics.

2. How Does the Calculator Work?

The calculator uses the beta equation, as shown in the image above:

\( R = R_0 \cdot e^{\beta \left( \frac{1}{T} - \frac{1}{T_0} \right)} \)

Where:

• \( R \): Resistance at target temperature \( T \);
• \( R_0 \): Nominal resistance at reference temperature \( T_0 \);
• \( \beta \): Beta value, a material constant (in Kelvin);
• \( T \): Target temperature (in Kelvin);
• \( T_0 \): Reference temperature (in Kelvin).

Steps:

• Enter the nominal resistance (\( R_0 \)) and select its unit (Ω, kΩ, MΩ).
• Enter the reference temperature (\( T_0 \)) and select its unit (°C or °F); defaults to 25°C.
• Enter the beta value (\( \beta \)) in Kelvin.
• Enter the target temperature (\( T \)) and select its unit (°C or °F).
• The calculator converts temperatures to Kelvin (\( T \text{ in K} = T \text{ in °C} + 273.15 \)), adjusts resistance units, and computes \( R \) using the beta equation.
• The result is formatted (scientific notation for values < 0.001, otherwise 4 decimal places) and displayed in the selected resistance unit.

3. Importance of NTC Thermistor Calculation

Calculating thermistor resistance is critical for:

• Temperature Sensing: Ensures accurate temperature measurements in circuits by predicting resistance changes.
• System Design: Helps design temperature compensation or monitoring systems in electronics.
• Calibration: Allows calibration of thermistors for specific temperature ranges in industrial or medical applications.

4. Using the Calculator

Example 1: Calculate the resistance of an NTC thermistor with \( R_0 = 10 \, \text{kΩ} \) at \( T_0 = 25 \, \text{°C} \), \( \beta = 3950 \, \text{K} \), at \( T = 50 \, \text{°C} \):

• \( R_0 \): 10 kΩ = 10000 Ω;
• \( T_0 \): 25°C = 298.15 K;
• \( T \): 50°C = 323.15 K;
• Exponent: \( \beta \left( \frac{1}{T} - \frac{1}{T_0} \right) = 3950 \left( \frac{1}{323.15} - \frac{1}{298.15} \right) \approx -0.5145 \);
• \( R \): \( 10000 \cdot e^{-0.5145} \approx 5982.6 \, \text{Ω} = 5.9826 \, \text{kΩ} \).

Example 2: Calculate the resistance of an NTC thermistor with \( R_0 = 10000 \, \text{Ω} \) at \( T_0 = 77 \, \text{°F} \), \( \beta = 3435 \, \text{K} \), at \( T = 32 \, \text{°F} \):

• \( R_0 \): 10000 Ω;
• \( T_0 \): 77°F = 25°C = 298.15 K;
• \( T \): 32°F = 0°C = 273.15 K;
• Exponent: \( 3435 \left( \frac{1}{273.15} - \frac{1}{298.15} \right) \approx 0.3142 \);
• \( R \): \( 10000 \cdot e^{0.3142} \approx 13690.6 \, \text{Ω} \).

5. Frequently Asked Questions (FAQ)

Q: How accurate is the beta equation for NTC thermistors?
A: The beta equation is an approximation and is most accurate over a narrow temperature range. For higher precision across a wider range, the Steinhart-Hart equation is preferred.

Q: Why are temperatures converted to Kelvin?
A: The beta equation requires temperatures in Kelvin because it models the exponential relationship of resistance with the inverse of absolute temperature.

Q: What is a typical beta value for NTC thermistors?
A: Beta values typically range from 2000 K to 5000 K, depending on the thermistor material. Common values are around 3435 K or 3950 K.

NTC Thermistor Calculator© - All Rights Reserved 2025